subtitle
  Post Categories
MachineLearning 44 Note 4 Tech 5 Life 3 Note 4 exercises 5
自相关图 自相关图
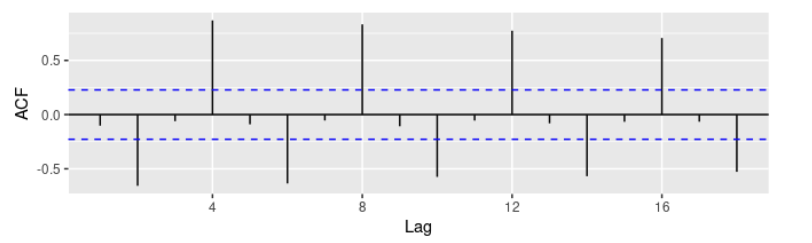
自相关系数自相关系数可以测量时间序列 滞后值 之间的线性相关性，正如相关系数可以衡量两个变量之间的线性相关性。 如 $r_1$ 衡量 $y_t$ 和 $y_{t-1}$ 之间的关系；$r_2$ 衡量 $y_t$ 和 $y_{t-2}$
2021-03-19 MachineLearning
时间序列 acf pacf
ARIMA 系列模型 ARIMA 系列模型
AR 模型自回归模型基于目标变量历史数据的组合对目标变量进行预测。自回归一词中的自字即表明其是对变量自身进行的回归。 一个 $p$ 阶的自回归模型 $AR(p)$可以表示如下：$$y_t=c+w_1y_{t-1}+w_2y_{t-2}+ …
2021-03-18 MachineLearning
arima ma ar
延迟算子 延迟算子
延迟算子时间序列的延迟使用延迟算子（backshift operator）描述， 用$B$ 表示。 (有的文献使用滞后算子，Lag operator，用$L$表示） $$By_t=y_{t-1}$$ $$B(By_t)=B^2y_t=y_{
2021-03-18 MachineLearning
时间序列
时间序列的平稳性 时间序列的平稳性
平稳性如果时间序列的性质不随时间变化而变化（如均值0，方差趋于稳定值），我们称该序列是平稳的。典型的平稳序列是白噪声（white noise series）。 因此具有趋势、周期性、季节性的序列不是平稳序列。 ARIMA模型要求序列是平稳的
2021-03-17 MachineLearning
arima 时间序列
Exploratory Data Analysis for Time Series Exploratory Data Analysis for Time Series
分两个部分，第一部分，讨论时间序列数据上常用的方法，如柱状图（histograms）、曲线图（plotting），和一些能用于时间序列数据的聚合操作（group-by operations）。 第二部分，重点讨论时间序列分析相关的方法。 F
2021-03-08 MachineLearning
时间序列 读书笔记
DeepAR: 使用自回归递归网络实现概率预测 DeepAR: 使用自回归递归网络实现概率预测
问题定义以商品销量举例， 第 $i$ 个商品在 $t$ 时刻的销量 $Z$ 表示为 $Z_{i, t}$； 我们预测条件分布 $P(Z_{i,t}|Z_{i, t-1}, Z_{i, t-2}, …, Z_{i, 1})$ 进一步预测更多
2021-03-03 MachineLearning
DeepAR 时间序列
时间序列的数学表示 时间序列的数学表示
任何按照时间顺序观察的事物都是时间序列。 以商品销量举例， 第 $i$ 个商品在 $t$ 时刻的销量 $Z$ 表示为 $Z_{i, t}$； 我们预测条件分布 $P(Z_{i,t}|Z_{i, t-1}, Z_{i, t-2}, …, Z
2021-03-03 MachineLearning
时间序列
逻辑回归 逻辑回归
逻辑回归（Logistic Regression）是一种常用于二分类问题的模型，又称对数几率回归（logit）。 为什么使用逻辑回归？我们使用线性回归，解决连续变量的预测问题。$$f(x) = WX$$ 其中 $W \in \R^n$是
2021-02-28 MachineLearning
逻辑回归
指示函数 指示函数
在集合论中，指示函数(Indicator function)是定义在某集合X上的函数，表示其中有哪些元素属于某一子集A。 集X的子集A的指示函数是函数${1_{A}:X\to \lbrace 0,1\rbrace }$ ，定义为: $$
2021-02-25 MachineLearning
概率
朴素贝叶斯 朴素贝叶斯
朴素贝叶斯方法是基于贝叶斯定于和特征条件独立假设的分类方法。 对于给定的训练数据集 首先基于条件独立假设学习输入输出的联合概率分布； 然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出 y。 朴素贝叶斯法优点 实
2021-02-24 MachineLearning
贝叶斯 概率
2 / 5