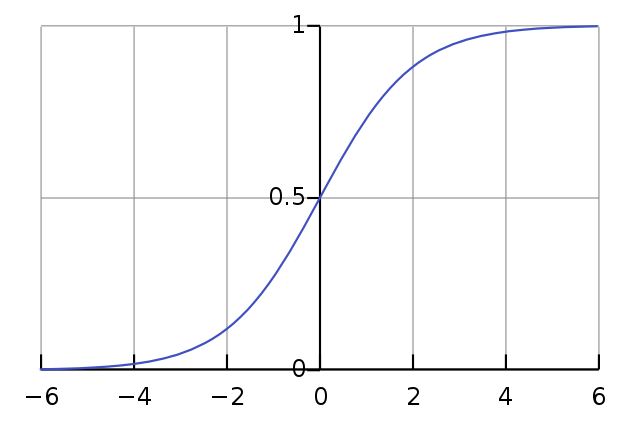
逻辑回归（Logistic Regression）是一种常用于二分类问题的模型，又称对数几率回归（logit）。 为什么使用逻辑回归？我们使用线性回归，解决连续变量的预测问题。$$f(x) = WX$$ 其中 $W \in \R^n$是

在集合论中，指示函数(Indicator function)是定义在某集合X上的函数，表示其中有哪些元素属于某一子集A。 集X的子集A的指示函数是函数${1_{A}:X\to \lbrace 0,1\rbrace }$ ，定义为: $$

朴素贝叶斯方法是基于贝叶斯定于和特征条件独立假设的分类方法。 对于给定的训练数据集 首先基于条件独立假设学习输入输出的联合概率分布； 然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出 y。 朴素贝叶斯法优点 实

在概率论中, 对两个随机变量X和Y，其联合分布 （Joint probability distribution） 是同时对于X和Y的概率分布。事件A 和B 同时发生概率记为 $P(A, B)$。 离散随机变量的联合分布对离散随机变量而言

在统计学中，最大似然估计（英语：Maximum Likelihood Estimation，简作MLE），也称极大似然估计，是用来估计一个概率模型的参数的一种方法。 频率学派 vs 贝叶斯学派频率学派与贝叶斯学派探讨「不确定性」这件事时

贝叶斯决策论贝叶斯决策论（Bayesian decision theory）是概率框架下实施决策的基本方法。 极大似然估计估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布，再基于训练样本对概率分布的参数进行估计。 朴素贝叶斯

源于托马斯·贝叶斯（Thomas Bayes）生前为解决一个“逆概”问题写的一篇文章，而这篇文章是在他死后才由他的一位朋友发表出来的。 什么叫逆概问题在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有N个白球，M个

讲解先验概率（Prior probability）和后验概率（Posterior probability）最好的方法是举例子。 例子 1一般情况下发生了交通事故，更容易堵车。 先验概率：今天出门堵车的可能性 $P(堵车)$ 条件概率

While training our model Bias and Variance plays a key role in achieving the required accuracy of the model.There need t

集成多个算法结果得到比任何单个算法更好的结果，称为集成学习。 常见的集成学习方法有： 贝叶斯最优分类器 Bootstrap aggregating（又称 Bagging）。代表算法随机森林。 Boosting。代表算法 AdaBoos