逻辑回归(Logistic Regression)是一种常用于二分类问题的模型,又称对数几率回归(logit)。
为什么使用逻辑回归?
我们使用线性回归,解决连续变量的预测问题。
$$
f(x) = WX
$$
其中 $W \in \R^n$是参数,$X \in R^n$ 是输入,$Y \in R$。
我们如何使用线性回归解决二元分类问题?即 $Y \in {0, 1}$
有很多种做法,我们使用逻辑函数缩放$Y$,让结果缩放在 (0, 1)。逻辑函数和改造后的模型分别如下:
$$
f(z) = \frac{1}{1 + e^{-z}}
$$
$$
f(x) = \frac{1}{1 + e^{WX}}
$$
$$
f(x)={\begin{cases}
\displaystyle \frac{1}{1 + e^{WX}} & Y_i=1, i=1,2,…N \\
1- \frac{1}{1 + e^{WX}} = \frac{e^{WX}}{1 + e^{WX}} & Y_i=0, i=1,2,…N
\end{cases}}
\\
= (\frac{1}{1+e^{WX}})^{y_i} * (1- \frac{1}{1+e^{WX}})^{1- y_i}, i=1,2,…N
$$
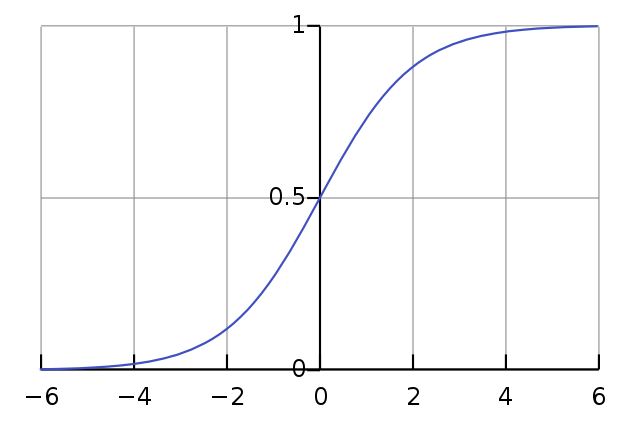
$f(x) \in (0, 1)$,输出的概率值越接近1,表示分类为1的可能性越高;输出的概率值越接近0,表示分类为0的可能性越高;
逻辑回归模型参数的估计
可以使用最大似然估计法估计模型的参数。
参考文献
- 《统计学习方法》- 李航

