使用 AR 和 ARIMA 模型预测比特币价格

使用比特币数据，预测未来7天比特币价格，演示 AR 和 ARIMA模型使用率高方法。

数据概览

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

df = pd.read_csv('arima/bitcoin_price_Training - Training.csv',parse_dates=['Date']).fillna(0)
df.head()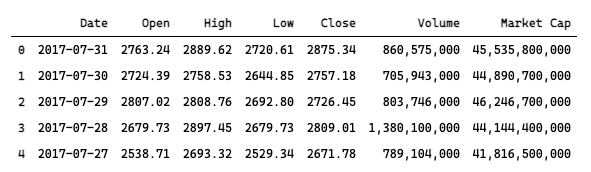

我们分析、预测的是比特币闭市价格 Close

# prepare time series data
ts = df[["Date", "Close"]].set_index("Date")
ts.sort_index(inplace=True)
ts = ts.Close
ts.head()

我们检测一下数据平稳性

from statsmodels.tsa.stattools import adfuller

adfuller_result = adfuller(ts)
if adfuller_result[1] > 0.05:
    print(f"p-value: {adfuller_result[1]}, not stationary")
else:
    print(f"p-value: {adfuller_result[1]}, stationary")

# p-value: 0.9990604352222925, not stationary

p-value: 0.99 数据不平稳，因此后文中我们实验拟合差分后的数据看看效果，具体查看 ARIMA(1,1,1) 模型部分。

画时序图，观察数据趋势、季节性、周期。

def time_plot_with_properties(ts, mean_window=24, std_window=12, figsize=(18, 12)):
    # calculate rolling mean
    rolled_mean = ts.rolling(window=mean_window, center=False).mean()
    # calculate rolling standard
    rolled_std = ts.rolling(window=std_window, center=False).std()

    _ = plt.figure(figsize=figsize)
    # time plot of the original series
    plt.plot(ts, color="blue", label="Original")
    # time plot of rolling mean
    if mean_window > 0:
        plt.plot(rolled_mean, color="red", label=f"Roll {mean_window} Mean")
    # time plot of standard Deviation
    if std_window > 0:
        plt.plot(rolled_std, color="black", label=f"Roll {std_window} Std")

    plt.xticks(rotation=90)
    plt.legend(loc="best")
    plt.title('Time Series Plot')
    plt.show(block=False)

time_plot_with_properties(ts)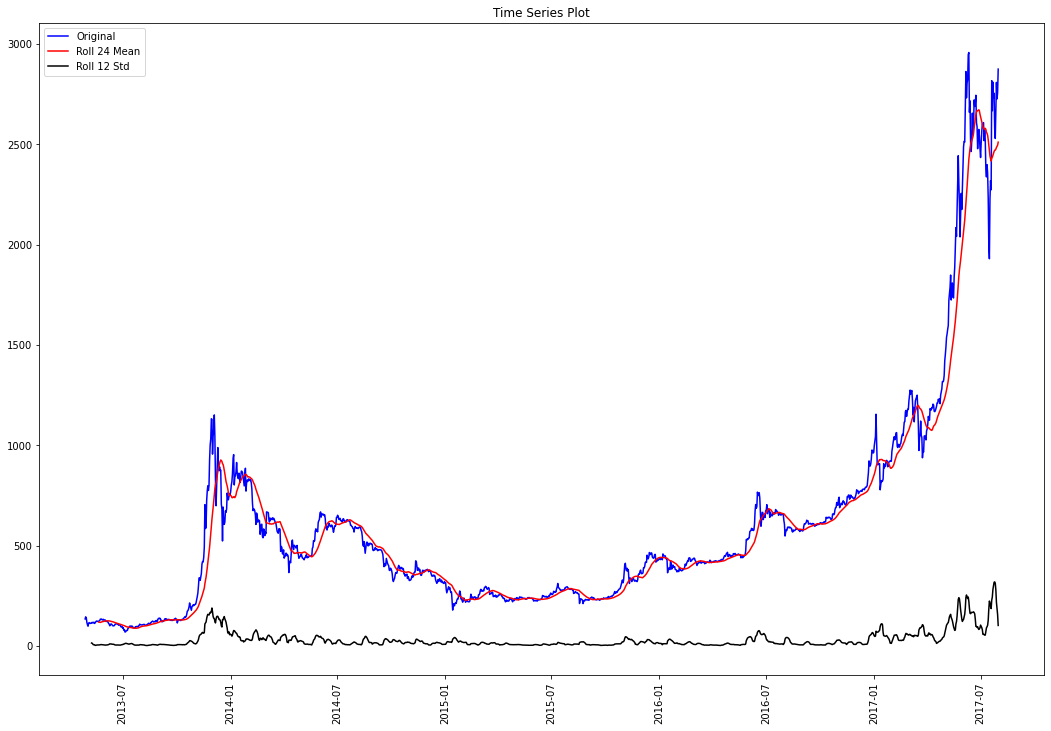

从时序图中观察到明显的上涨趋势。

画 acf、pacf 图

import statsmodels.api as sm

# time warning 47 seconds
_ = plt.figure(figsize=(18, 12))
ax1 = plt.subplot(211)
sm.graphics.tsa.plot_acf(ts, lags=150, ax=ax1)
ax2 = plt.subplot(212)
sm.graphics.tsa.plot_pacf(ts, lags=150, ax=ax2)
plt.show()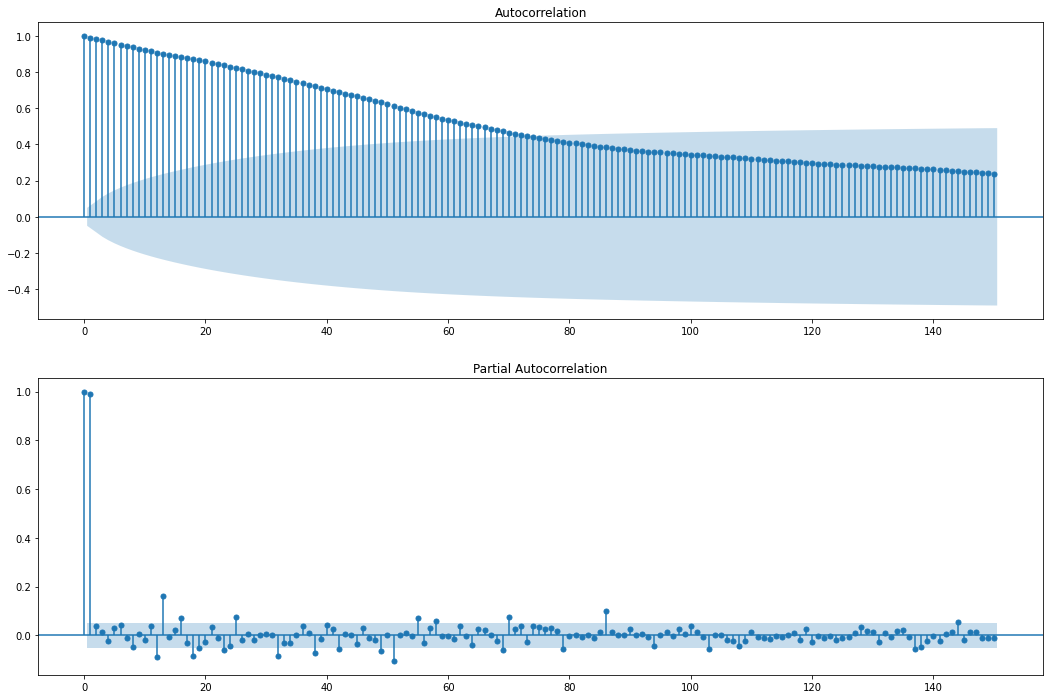

1. pacf 图中 Lag0 和 LagN 不在一个数量级，影响观察。
2. 考虑到比特币价格数据，在时间上可能有周期性（如这周一和上周一可能有某种相关性），因此我们先做 1 阶差分去除 Lag0

ts_diff1 = ts - ts.shift()
ts_diff1.dropna(inplace=True)

# time warning 47 seconds
_ = plt.figure(figsize=(18, 12))
ax1 = plt.subplot(211)
sm.graphics.tsa.plot_acf(ts_diff1, lags=150, ax=ax1)
ax2 = plt.subplot(212)
sm.graphics.tsa.plot_pacf(ts_diff1, lags=150, ax=ax2)
plt.show()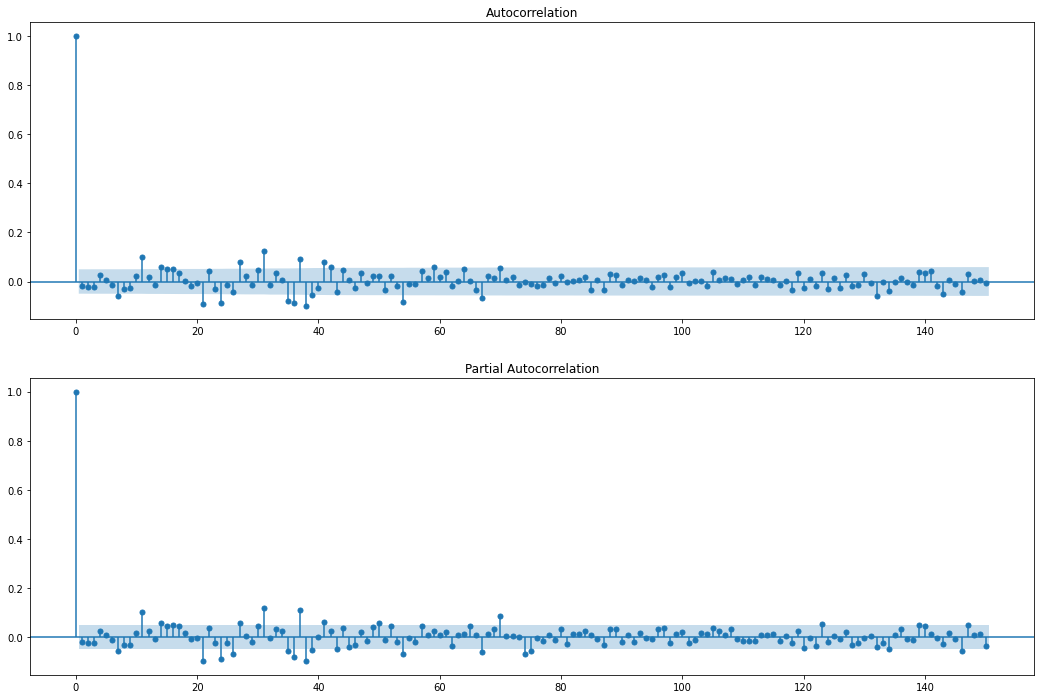

1. acf 可观察到明显的周期性
2. acf 在 17、18 阶截尾; q 取值搜索范围 [17, 18]
3. pacf 拖尾，且有周期性; p 取值搜索范围 [1, 8, 11, 14, 15, 20, 22, 25, 29, 30, 31, 36, 43]

切分数据集

test_size = 100
y_train, y_test = ts[0:-test_size], ts[-test_size:]
print(y_train.shape, y_test.shape)s

p_lst = [[1, 8, 11, 14, 15, 20, 22, 25, 29, 30, 31, 36, 43]]
d = 1
q_lst = [17, 18]
result_lst = []

for p in p_lst:
    for q in q_lst:
        model = ARIMA(y_train, order=(p, d, q))
        model_fitted = model.fit()
        rss = sum((model_fitted.fittedvalues - ts_log_diff1.Close) ** 2)
        result = {
            "p": p,
            "d": d,
            "q": q,
            "rss": rss,
            "aic": model_fitted.aic,
            "bic": model_fitted.bic,
            "hqic": model_fitted.hqic,
        }
        print(result)
        result_lst.append(result)

搜索过程很耗时间，下文举例的模型中使用 p=1, d=[0,1], q=1。

$ARIMA(1, 0, 1)$ 模型实验

from statsmodels.tsa.arima_model import ARIMA

model_fitted = ARIMA(y_train, order=(1, 0, 1)).fit()

print(model_fittedsummary())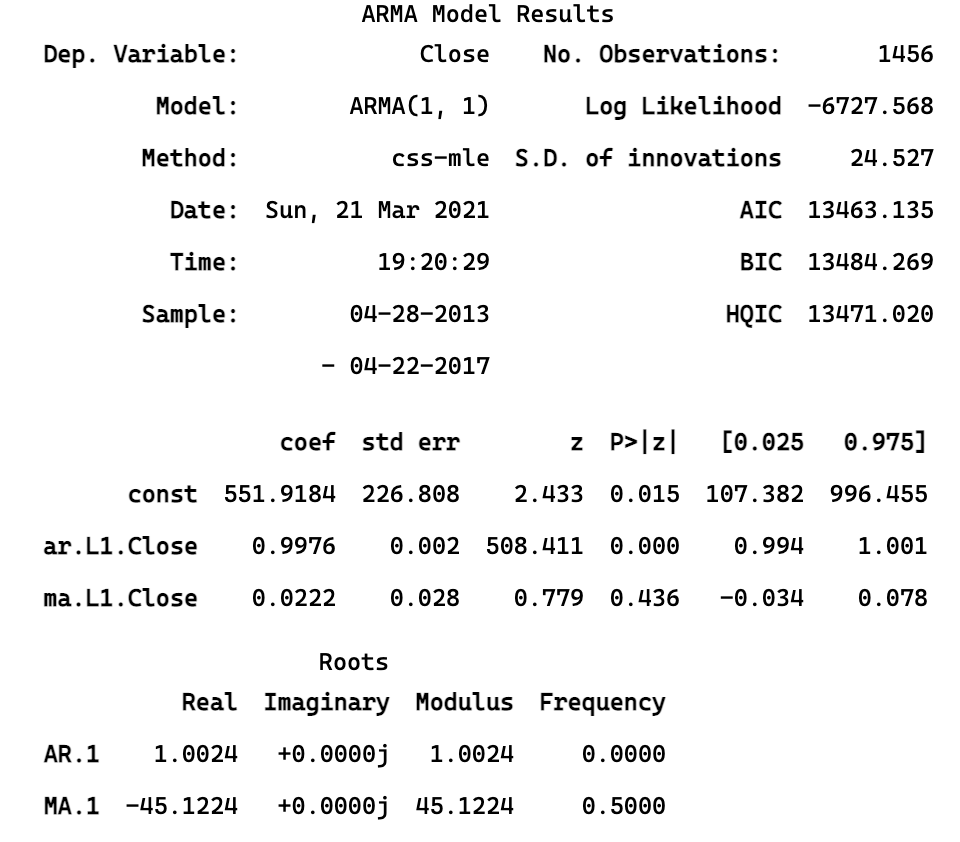

$$
y_t = 551.9184 + 0.9976*y_{t-1} + 0.0222 * \epsilon_{t-1}
$$

验证集上的效果

report = pd.DataFrame(columns=["actual", "prediction", "bias", "accuracy"])

report["actual"] = y_train[1:]
report["prediction"] = model_fitted.fittedvalues
report["bias"] = np.abs(report["actual"] - report["prediction"])
report["accuracy"] = 1 - report["bias"]/report.actual

accuracy_all = 1- report.bias.sum()/report.actual.sum()
print(accuracy_all)
# 0.9743485267660159
report.head()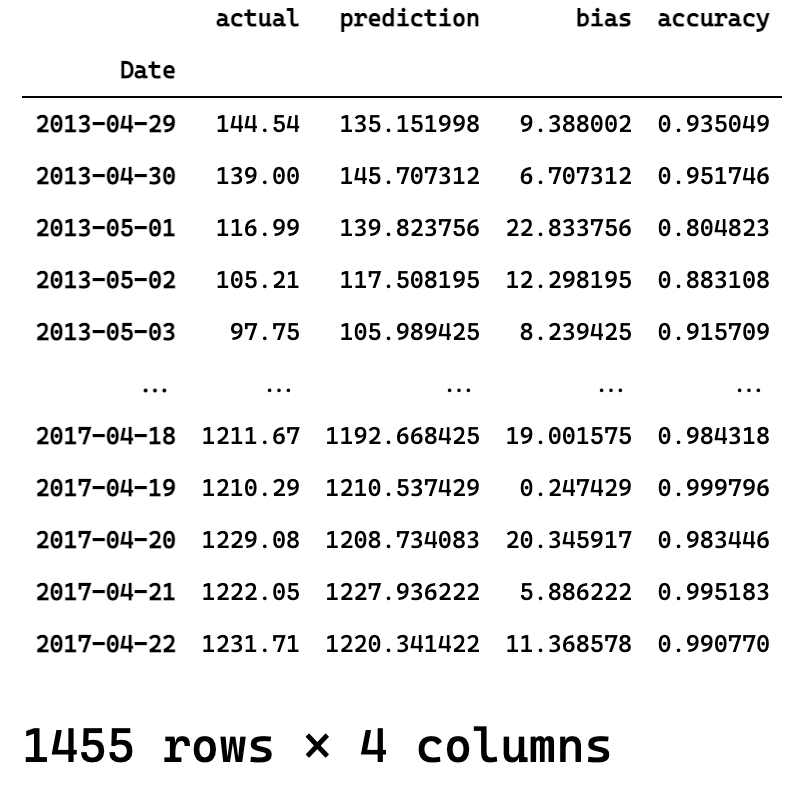

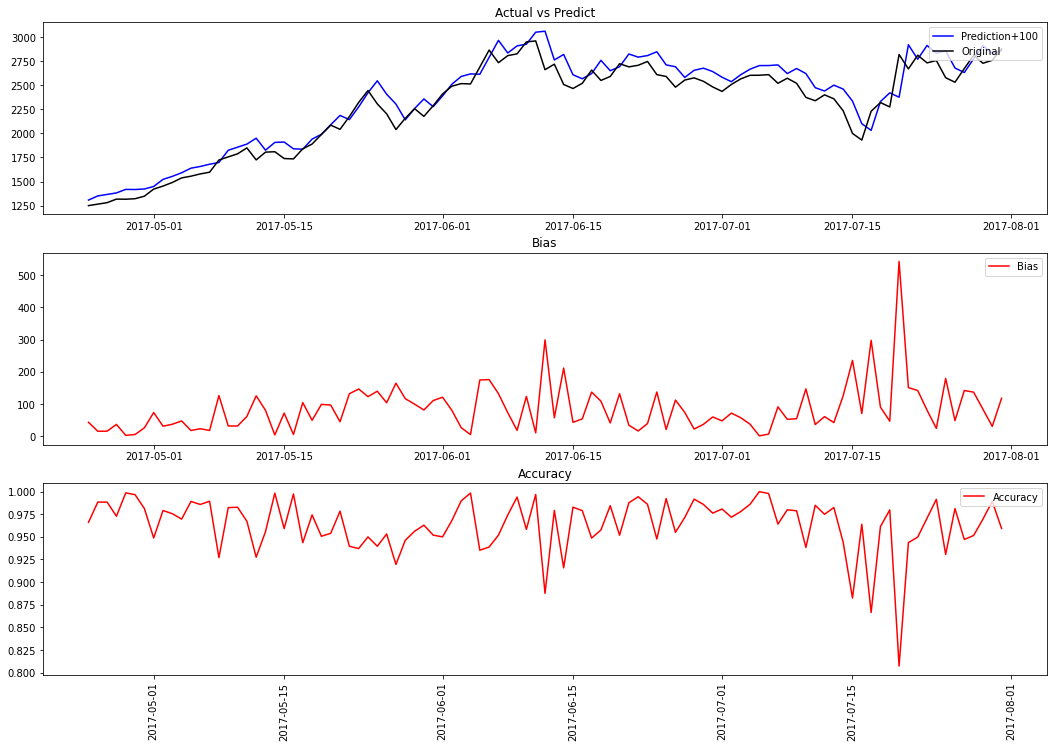
验证集拟合效果很好

_ = plt.figure(figsize=(18, 12))
ax1 = plt.subplot(311)
plt.plot(report["prediction"]+100, '-', color="blue", label="Prediction+100")
plt.plot(report["actual"], color="black", label="Actual")
plt.title('Actual vs Predict')
plt.legend(loc="upper right")

ax2 = plt.subplot(312)
plt.plot(report["bias"], color="red", label="Bias")
plt.title('Bias')
plt.legend(loc="upper right")

ax3 = plt.subplot(313)
plt.plot(report["accuracy"], color="red", label="Accuracy")
plt.xticks(rotation=90)
plt.legend(loc="upper right")

plt.title('Accuracy')
plt.show(block=False)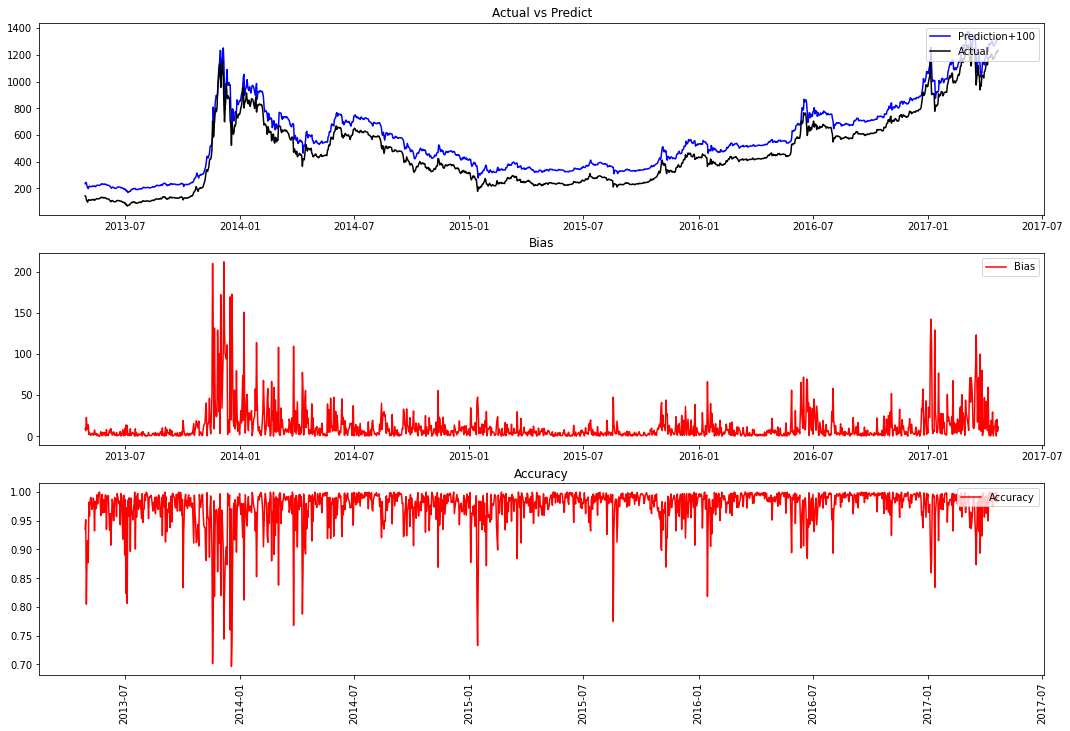

$ARIMA(1,1,1)$

model_fitted = ARIMA(y_train, order=(1, 1, 1)).fit()

print(model_fittedsummary())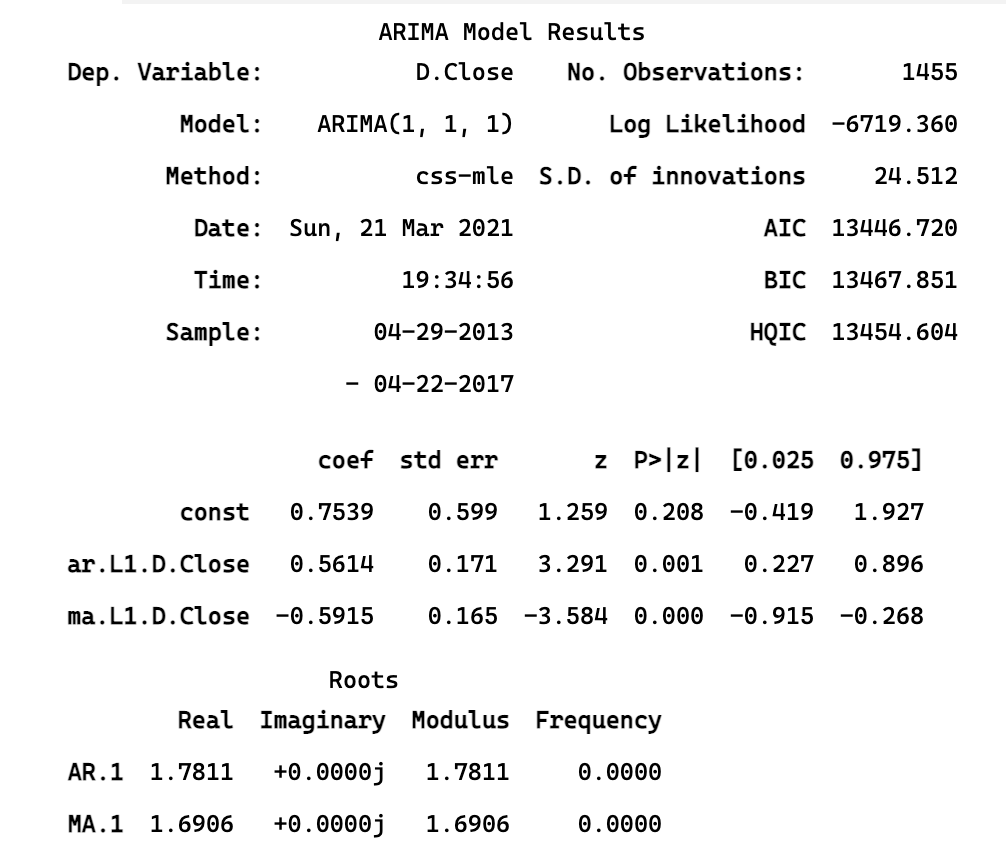

注意模型预测的 y’，也就是是说 model_fitted.fittedvalues 输出的是 y’

$$
y_t’ = 0.753 + 0.5614*y_{t-1}’ - 0.5915 * \epsilon_{t-1}
$$

验证集上的效果

report = pd.DataFrame(columns=["actual", "prediction", "bias", "accuracy"])

report["actual"] = y_train[1:]
# 注意模型预测的 y'，也就是是说 model_fitted.fittedvalues 输出的是 y'
report["prediction"] = fitted_values = y_train.shift(1) + model_fitted.fittedvalues
report["bias"] = np.abs(report["actual"] - report["prediction"])
report["accuracy"] = 1 - report["bias"]/report.actual

accuracy_all = 1- report.bias.sum()/report.actual.sum()
print(accuracy_all)
# 0.9744896568566263
report.head()

验证集拟合效果很好

_ = plt.figure(figsize=(18, 12))
ax1 = plt.subplot(311)
plt.plot(report["prediction"]+100, '-', color="blue", label="Prediction+100")
plt.plot(report["actual"], color="black", label="Actual")
plt.title('Actual vs Predict')
plt.legend(loc="upper right")

ax2 = plt.subplot(312)
plt.plot(report["bias"], color="red", label="Bias")
plt.title('Bias')
plt.legend(loc="upper right")

ax3 = plt.subplot(313)
plt.plot(report["accuracy"], color="red", label="Accuracy")
plt.xticks(rotation=90)
plt.legend(loc="upper right")

plt.title('Accuracy')
plt.show(block=False)

使用 ARIMA(1,1,1) 预测未来数据

model_fitted = ARIMA(y_train, order=(1, 1, 1)).fit()

y_diff = model_fitted.predict(start="2017-04-23", end="2017-07-31", dynamic=True)

y_diff.head()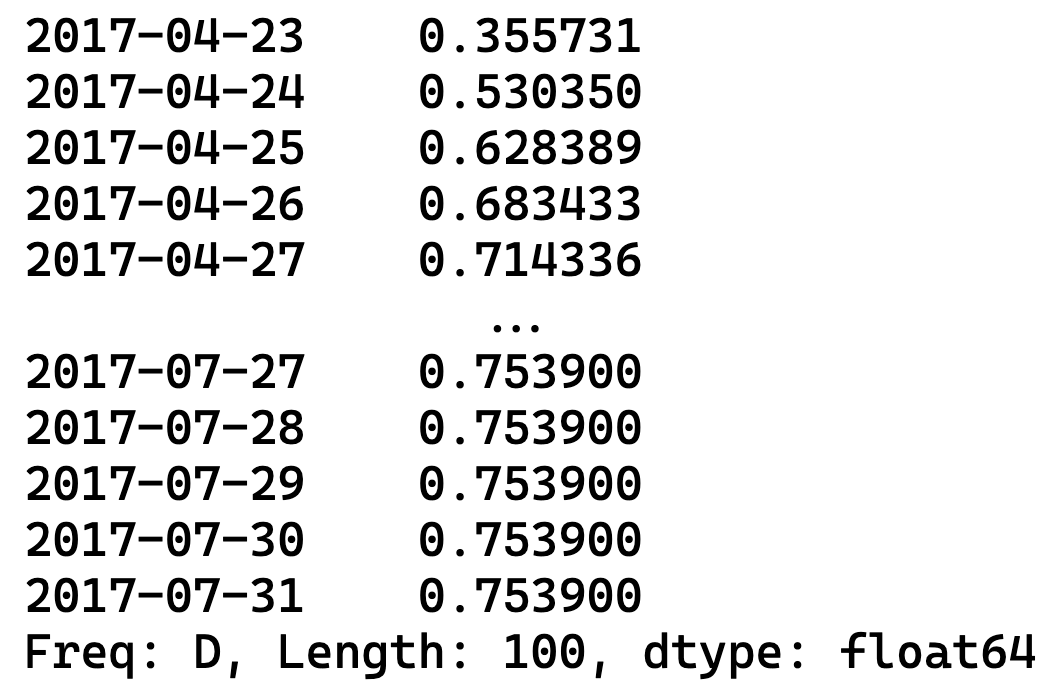

report = pd.DataFrame(columns=["actual", "prediction", "bias", "accuracy"])

report["actual"] = y_test[1:]
# 注意模型预测的 y'，也就是是说 model_fitted.fittedvalues 输出的是 y'
report["prediction"] = (y_test + y_diff).shift()
report["bias"] = np.abs(report["actual"] - report["prediction"])
report["accuracy"] = 1 - report["bias"]/report.actual

accuracy_all = 1- report.bias.sum()/report.actual.sum()
print(accuracy_all)
# 0.9630198002158743
report.head()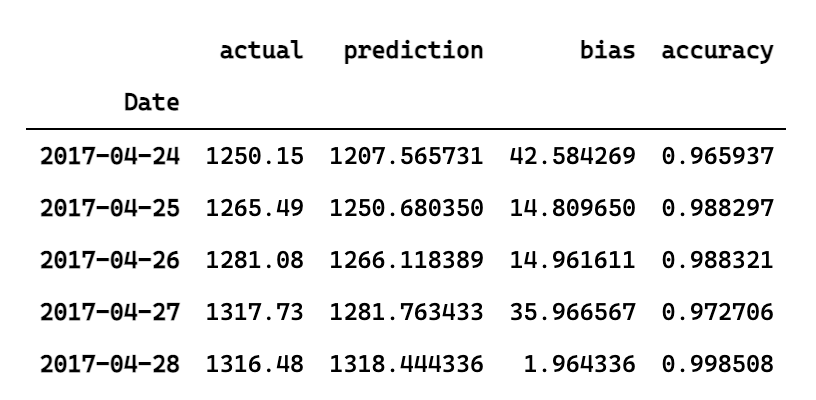

_ = plt.figure(figsize=(18, 12))
ax1 = plt.subplot(311)
plt.plot(report["prediction"]+100, '-', color="blue", label="Prediction+100")
plt.plot(report["actual"], color="black", label="Actual")
plt.title('Actual vs Predict')
plt.legend(loc="upper right")

ax2 = plt.subplot(312)
plt.plot(report["bias"], color="red", label="Bias")
plt.title('Bias')
plt.legend(loc="upper right")

ax3 = plt.subplot(313)
plt.plot(report["accuracy"], color="red", label="Accuracy")
plt.xticks(rotation=90)
plt.legend(loc="upper right")

plt.title('Accuracy')
plt.show(block=False)