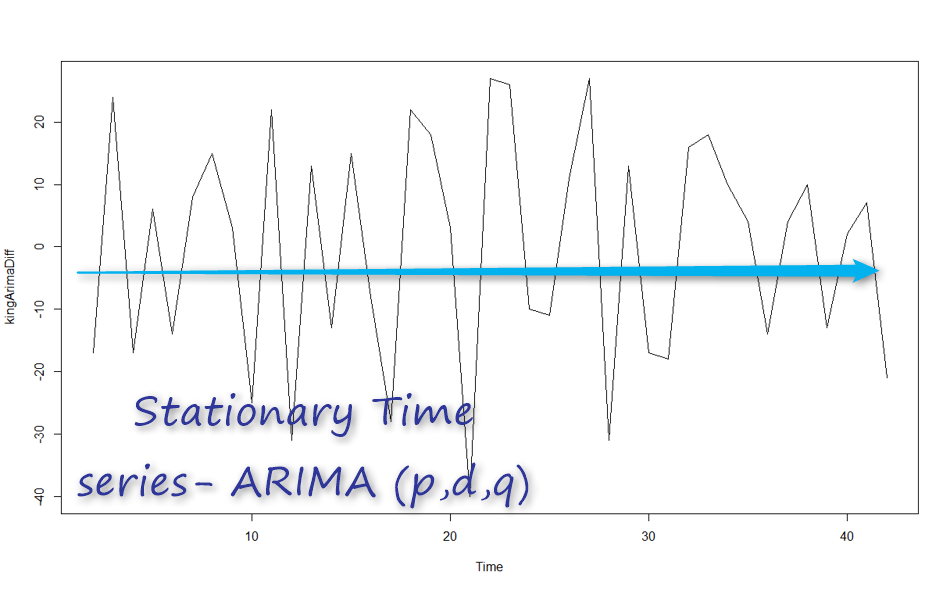
自相关系数
自相关系数可以测量时间序列 滞后值 之间的线性相关性,正如相关系数可以衡量两个变量之间的线性相关性。
如 $r_1$ 衡量 $y_t$ 和 $y_{t-1}$ 之间的关系;$r_2$ 衡量 $y_t$ 和 $y_{t-2}$ 之间的关系。
$$
r_k=\frac{\sum_{t=k+1}^{T}(y_t-\hat{y})(y_{t-k}-\hat{y})}{\sum_{t=1}^{T}(y_t-\hat{y})^2}
$$
其中,$\hat{y}$ 是均值,$T$ 是序列长度。
通过绘制自相关系数图可以描绘 $自相关函数$ 或者是 $ACF$。
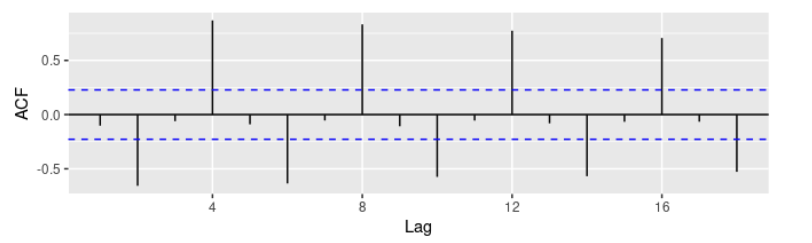
在该图中:
- $r_4$ 值最大。这是由于数据的季节性形态:顶峰往往出现在第四季度,谷底往往出现在第二季度。
- $r_2$ 值最小。这是由于谷底往往在高峰之后的两个季度出现。
- 蓝色虚线之内的区域自相关性可近似看做 0。
偏子相关
现在如果 $yt$ 和 $y_{t−1}$ 已经存在相关性,则 $y_{t−1}$ 和 $y_{t−2}$ 必然存在相关性。然而 $yt$ 和 $y_{t−2}$ 也同样必然相关,这是因为它们都与 $y_{t−1}$ 相关而不是因为 $y_{t−2}$ 包含新的信息可以用来预测 $y_t$。
为了解决这个问题,我们可以使用偏自相关, partial autocorrelations 简称 PACF。
偏自相关衡量的是在移除延迟 $1,2,3,…,k−1$ 对 $y_t$ 的影响的情况下, $y_t$ 和 $y_{t−k}$ 的关系。
因此延迟一阶偏自相关系数和延迟一阶自相关系数是相同的,因为没有延迟需要移除。
每个偏自相关系数都可以被估计为一个自回归模型中的末项系数。
特别地,$\alpha_k$ 作为第 k 个偏自相关系数,等于在一个 $AR(k)$ 模型中 $w_k$ 的估计值。
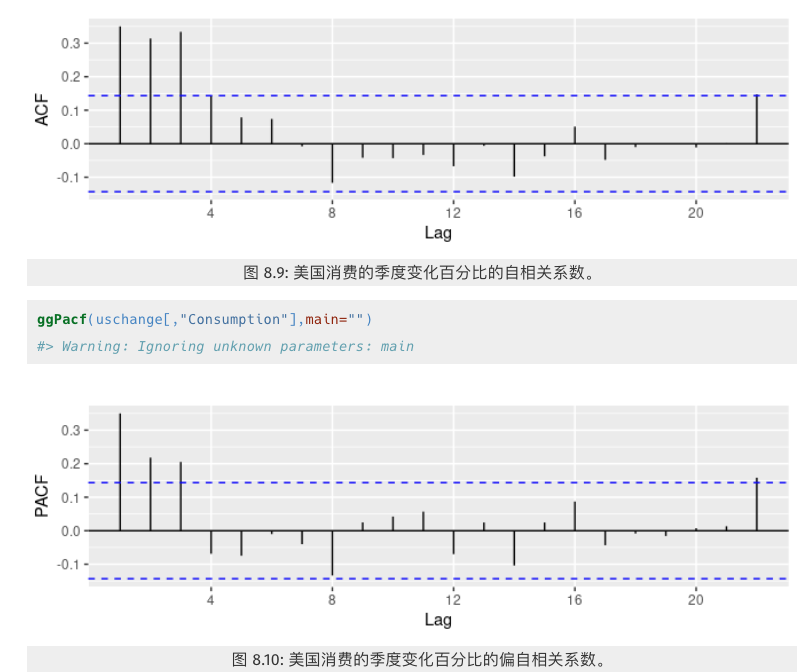
ACF 图中的趋势性和季节性
当数据具有趋势性时,短期滞后的自相关值较大,因为观测点附近的值波动不会很大。
当数据具有季节性时,自相关值在滞后阶数与季节周期相同时(或者在季节周期的倍数)较大。
当数据同时具有趋势和季节性时,我们会观察到组合效应。如下图
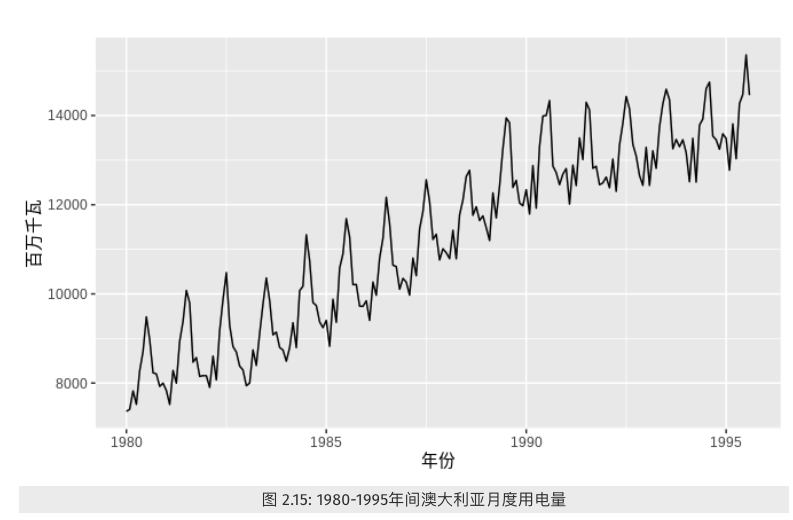
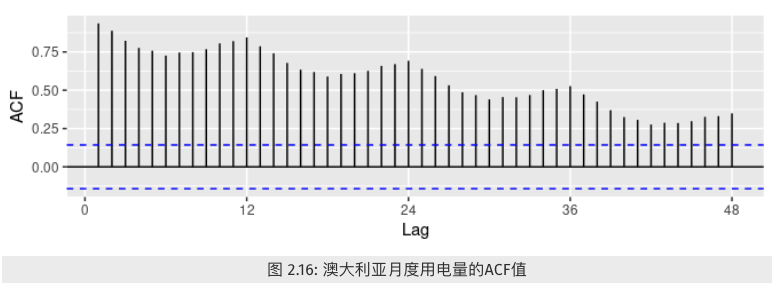
- 因为原时间序列中具有趋势变化,自相关系数值随着滞后阶数增加而缓慢降低。
- 原时间序列中的季节性变化,图中出现“圆齿状”形状。
白噪声
白噪声是一个对所有时间其自相关系数为零的随机过程。
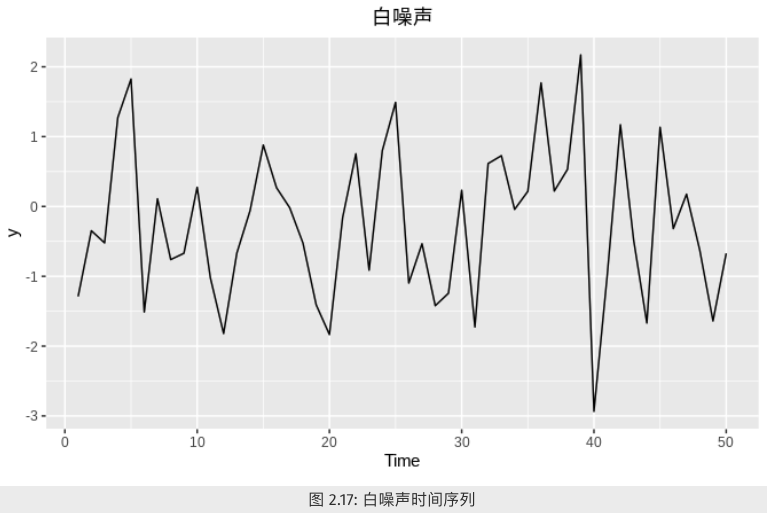
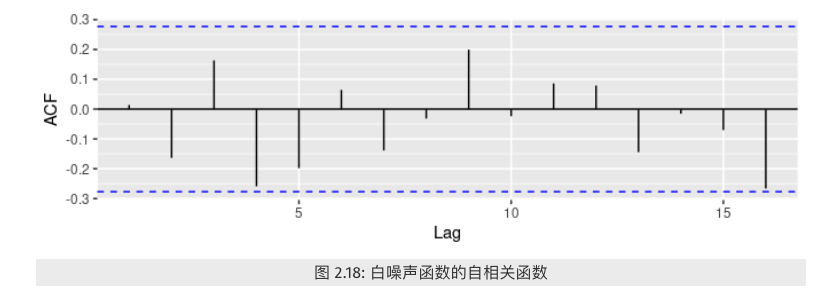
对于白噪声而言,我们期望它的自相关值接近0。
- 但是由于随机扰动的存在,自相关值并不会精确地等于0。
- 对于一个长度为 $T$ 的白噪声序列而言,我们期望在0.95 的置信度下,它的自相关值处于 $\frac{\pm2}{\sqrt{T}}$ 之间。
- 我们可以很容易的画出ACF的边界值(图中蓝色虚线)。
- 如果一个序列中有较多的自相关值处于边界之外,那么该序列很可能不是白噪声序列。