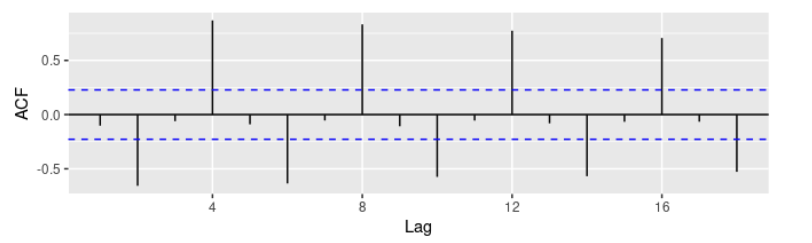
单位根检验

单位根检验

单位根检验是一种更客观的判定是否需要差分的方法。

这个针对平稳性的统计假设检验被用于判断是否需要差分方法来让数据更平稳。
单位根检验的方法有很多种，ADF是一种常用的单位根检验方法，他的原假设为序列具有单位根，即非平稳，对于一个平稳的时序数据，就需要在给定的置信水平上显著拒绝原假设。

ADF 检验

在统计学里，迪基-福勒检验（Dickey-Fuller test）可以测试一个自回归模型是否存在单位根（unit root）。

ADF 检验思路：

1. ADF 测试提出虚无假设（Null hypothesis, H0）：存在单位根；产生对立假设（Alternative Hypothesis, H1）。
2. 计算对比 ADF 统计量和给定显著性水平下的ADF统计量的临界值，从而得出虚无假设被拒绝的概率。

如果存在单位根，序列不平稳，原因如下。（不关心单位根不存在的情况，因为如果不存在，并不能说明平稳或不平稳）

一个简单的 $AR(1)$ 模型如下：

$$
y_t=w_1y_{t-1} + \epsilon_t
$$
其中，$\epsilon_t$ 是平稳序列（如白噪声）。

一阶差分：
$$
y_t’=y_t-y_{t-1}=(w_1y_{t-1} + \epsilon_t)-y_{t-1}=(w_1-1)y_{t-1}+\epsilon_t
$$

假设 $w_1=1$ （即单位根存在），一阶差分是平稳序列：

$$
y_t’=\epsilon_t
$$

于是，$y_t$ 是非平稳序列，相当于随机游走（random walk）：
$$
y_t = y_{t-1} + \epsilon_t=y_0 +\sum_{i=1}^{t}\epsilon_i
$$

使用 ADF 结果判断平稳性

ADF 检验结果，可能如下：

test_result = (
    -0.4801283240847767,
    0.8958363331790191,
    13,
    1542,
    {
        "1%": -3.4345978724183603,
        "5%": -2.863416175501975,
        "10%": -2.567768846731635,
    },
    -6789.599195492883,
)

• 第一个值，-1.8481210964862593 是显著性检验统计量（tau-statistic Critical value）。
• 第二个值， 0.35684591783869046 是 p-value，虚无假设不被拒绝（注：不等于成立）的概率。
• 第三个值，0 是使用的滞后阶数。（The number of lags used.）
• 第四个值，用于ADF回归和计算临界值用到的观测值数目。
• 第五个值，三个置信度。Critical values for the test statistic at the 1%, 5%, 10% levels. Based on MacKinnon (2010)

两种方法可以判断平稳性，

方法一、观察 p-value ：

• 如果 p-value 很大（p-value>0.05），说明虚无假设不被拒绝（注：不等于成立）的概率很大。即大概率存在单位根，序列非平稳。
• 如果 p-value 很小（p-value <= 0.05），说明虚无假设被拒绝。即小概率存在（相当于不存在）单位根，不存在单位根情况下，无法确定平稳性。

方法二、比较显著性检验统计量（au-statistic Critical value）和三个置信度上的统计量：

• 如果显著性检验统计量大于三个置信度上的值，说明虚无假设不被拒绝（注：不等于成立）。即存在单位根，序列非平稳。
• 如果显著性检验统计量小于任意一个置信度上的值，说明虚无假设被拒绝。即不存在单位根，无法确定平稳性序列平稳。

示例

使用比特币价格数据（来自 Kaggle 数据集）

import pandas as pd

df = pd.read_csv('arima/bitcoin_price_Training - Training.csv',parse_dates=['Date']).fillna(0)
df.head()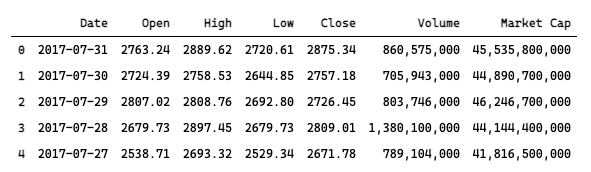

其中，闭市价格 Close 是我们分析对象。

ts = df[["Date", "Close"]].set_index("Date")
ts.sort_index(inplace=True)
ts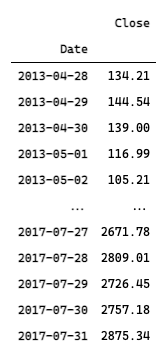

先观察时序图

from matplotlib import pyplot as plt

def time_plot_with_properties(ts, mean_window=24, std_window=12):
    # calculate rolling mean
    rolled_mean = ts.rolling(window=mean_window, center=False).mean()
    # calculate rolling standard
    rolled_std = ts.rolling(window=std_window, center=False).std()

    _ = plt.figure(figsize=(18, 12))
    # time plot of the original series
    plt.plot(ts, color="blue", label="Original")
    # time plot of rolling mean
    plt.plot(rolled_mean, color="red", label=f"Roll {mean_window} Mean")
    # time plot of standard Deviation
    plt.plot(rolled_std, color="black", label=f"Roll {std_window} Std")

    plt.xticks(rotation=90)
    plt.legend(loc="best")
    plt.title('Rolling Mean & Standard Deviation')
    plt.show(block=False)

time_plot_with_properties(ts)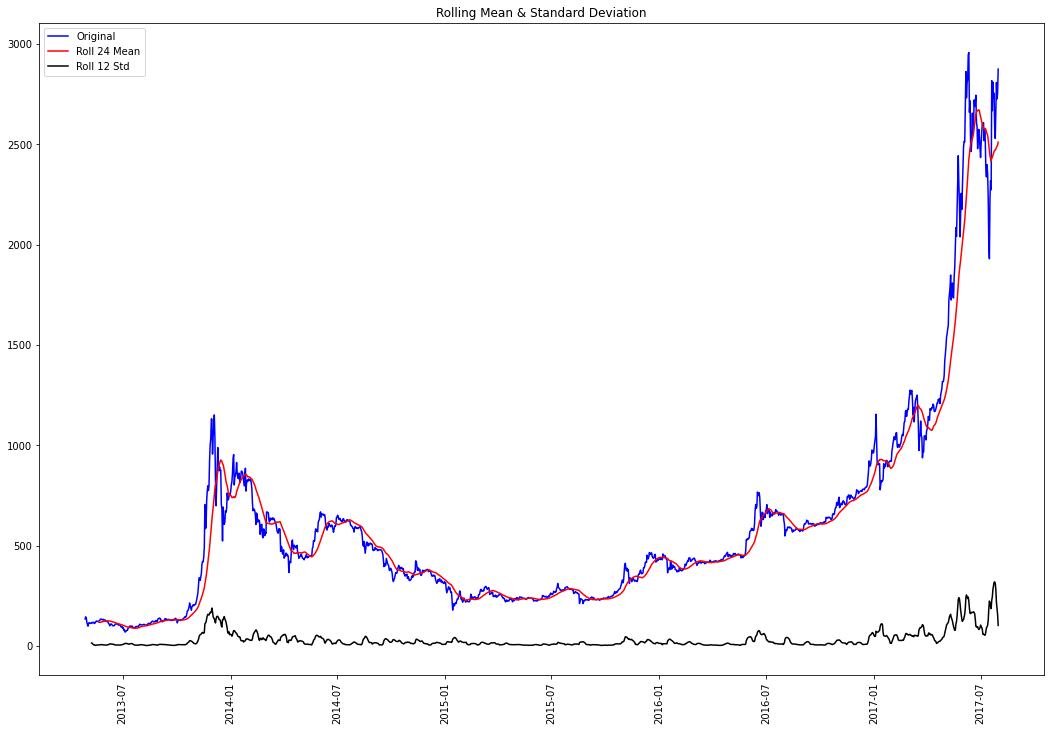

Augmented Dickey Fuller Test

from statsmodels.tsa.stattools import adfuller

test_result = adfuller(ts)
print(test_result)

ADF 结果如下

test_result = (
    2.535588587388622,
    0.9990604352222925,
    24,
    1531,
    {
        "1%": -3.4346284441307184,
        "5%": -2.863429668579316,
        "10%": -2.5677760318409732,
    },
    15393.063847184316,
)

方法一、观察 p-value ：

• p-value=0.9990604352222925 很大，虚无假设不被拒绝的概率很大，序列非平稳。

方法二、比较显著性检验统计量（au-statistic Critical value）和三个置信度上的统计量：

• critical_value=2.535588587388622 大于三个置信度上的值（-3.4, -2.8, -2.5），虚无假设不被拒绝的概率很大，序列非平稳。

两种方法得出结论一致，改序列不平稳。