AR 模型
自回归模型基于目标变量历史数据的组合对目标变量进行预测。自回归一词中的自字即表明其是对变量自身进行的回归。
一个 $p$ 阶的自回归模型 $AR(p)$可以表示如下:
$$
y_t=c+w_1y_{t-1}+w_2y_{t-2}+ … +w_py_{t-p}+ \epsilon_t
$$
$$
=c+ \sum_{i=1}^pw_iy_{t-i} + \epsilon_t
$$
其中,$c$是常数,$\epsilon_t$ 是白噪声序列。
$AR(p)$ 相当于$y$ 自己历史值的多元回归。
如 $AR(1)$ 模型:
$$y_t=c+w_1y_{t-1} + \epsilon_t$$
- 当 $w_1=0$ 时,$y_t$相当于白噪声;
- 当 $w_1=1, c=0$ 时,$y_t$相当于随机游走模型(random walk);
- 当 $w_1<0$ 时,$y_t$相当于倾向于在正负值之间上下浮动。
我们通常将自回归模型的应用限制在平稳数据上。
AR 模型优点与限制
自回归方法的优点是所需数据不多,可用自身历史数据来进行预测。
但也有如下限制:
- 要求数据是平稳的。
- 历史数据必须具有自相关性,自相关系数$w_i$是关键。如果自相关系数(R)小于0.5,则不宜采用,否则预测结果极不准确。
- 无法采集其他变量信息。对于受社会因素影响较大的经济现象,不宜采用自回归,而应改采用可纳入其他变量的向量自回归模型(英语:Vector Autoregression model,简称VAR模型)。
MA 模型
移动平均模型(moving average model)使用历史预测误差来建立一个类似回归的模型。
$MA(q)$表示为:
$$
y_t=c+w_1\epsilon_{t-1}+w_2\epsilon_{t-2}+ … +w_q\epsilon_{t-q}+ \epsilon_t
$$
$$
=c+ \sum_{i=1}^qw_iy_{t-i} + \epsilon_t
$$
$y_t$ 的每一个值都可以被认为是一个历史预测误差的加权移动平均值。
MA模型和移动平均平滑法 的区别:
- 移动平均模型是用于预测未来值的方法,
- 而移动平均平滑法(Moving average smoothing)则是用来估计历史值的循环趋势
移动平均模型的优缺点
使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响。
但移动平均法运用时也存在着如下问题:
- 要求数据是平稳的。
- 加大移动平均法的期数(即加大q值)会使平滑波动效果更好,但会使预测值对数据实际变动更不敏感;
- 移动平均值并不能总是很好地反映出趋势。由于是平均值,预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动;
非季节性ARIMA模型
将差分和自回归模型以及移动平均模型结合起来的时候,我们可以得到一个非季节性 ARIMA 模型。
ARIMA 全称自回归移动平均模型 (Auto Regressive Integrated Moving Average),是统计模型(statistic model)中最常见的一种用于时间序列预测的模型。(在这里Integrated指的是差分的逆过程) 。
ARIMA 模型要求数据是稳定序列。
指数平滑模型(exponential smoothing)和ARIMA模型是应用最为广泛的两种。基于对这两种预测方法的拓展,很多其他的预测方法得以诞生。
与指数平滑模型针对于数据中的趋势(trend)和季节性(seasonality)不同,ARIMA模型旨在描绘数据的自回归性(autocorrelations)。
ARIMA(q,d,q) 模型的特例: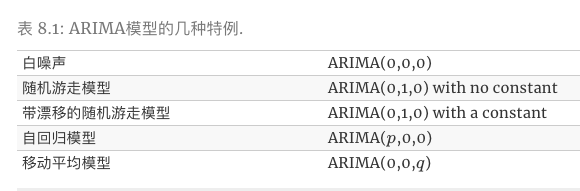
ARIMA 建模流程:
- 画出数据时序图并检查有无异常观测。
- 如果必要的话,对数据进行变换(如 Box-Cox 变换)来稳定方差。
- 如果数据非平稳,对数据进行差分直到数据平稳。
- 选择合适的 $p和q$ 的取值。
- 估计模型参数。
- 一旦我们确定了模型的阶数(p,d,q的取值),我们就需要估计参数 $c、w_1,…,w_p,、\beta_1,…,\beta_q$ 了。
- 可以使用极大似然估计 (maximum likelihood estimation) ,最大化观测到的数据出现的概率来确定参数;或使用最小二乘估计,通过最小化方差确定参数。
- 假设检验,判断残差序列是否为白噪声序列。
- 通过画出残差自相关图来检查你选择模型的残差,并且对残差进行一元混成检验(portmanteau test)或Box-Pierce方法检验。
- 如果它们看起来不像白噪声,那么模型就需要修正。(我们知道一个好的模型fitting出来的结果应该要是 stationary。)
- 如果残差是白噪声,利用已通过检验的模型进行预测。
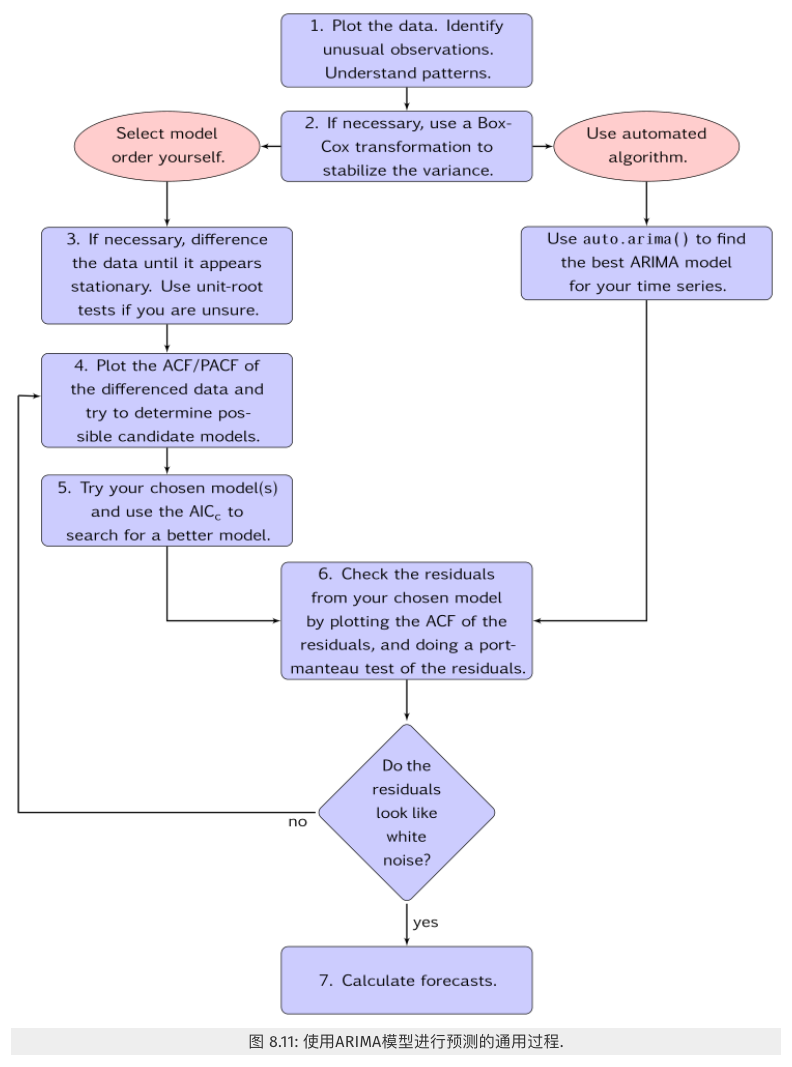
其中第4步,介绍两种常用的方法:
- 观察 acf, pacf 图,人工确定可能的 p,q取值
- 遍历p,q的取值,选择最小化 AIC/BIC(信息注册函数) 的p,q 取值。如 Hyndman-Khandakar 算法。
实际应用中,这两种方法可以混用,如
- 先通过 Hyndman-Khandakar算法自动调参,然后通过 ACF/PACF图检验、修正 p、q取值。
- 或先观察 ACF,PACF图,选出几个可能的 p,q取值,然后计算 AIC,选择误差最小的。
自相关图和偏自相关图
仅从时序图中我们通常无法判断 $p和q$ 的合适取值。然而我们有时从自相关图和与其紧密相关的偏自相关图中,可以判断 $p和q$ 的合适取值。
自相关图(ACF Plot)反映了自回归中 $y_t$ 和 $y_{t−k}$ 在不同 k 取值之下的关系。
现在如果 $yt$ 和 $y_{t−1}$ 已经存在相关性,则 $y_{t−1}$ 和 $y_{t−2}$ 必然存在相关性。然而 $yt$ 和 $y_{t−2}$ 也同样必然相关,这是因为它们都与 $y_{t−1}$ 相关而不是因为 $y_{t−2}$ 包含新的信息可以用来预测 $y_t$。
为了解决这个问题,我们可以使用偏自相关, partial autocorrelations 简称 PACF。
偏自相关衡量的是在移除延迟 $1,2,3,…,k−1$ 对 $y_t$ 的影响的情况下, $y_t$ 和 $y_{t−k}$ 的关系。
因此延迟一阶偏自相关系数和延迟一阶自相关系数是相同的,因为没有延迟需要移除。
每个偏自相关系数都可以被估计为一个自回归模型中的末项系数。
特别地,$\alpha_k$ 作为第 k 个偏自相关系数,等于在一个 $AR(k)$ 模型中 $w_k$ 的估计值。
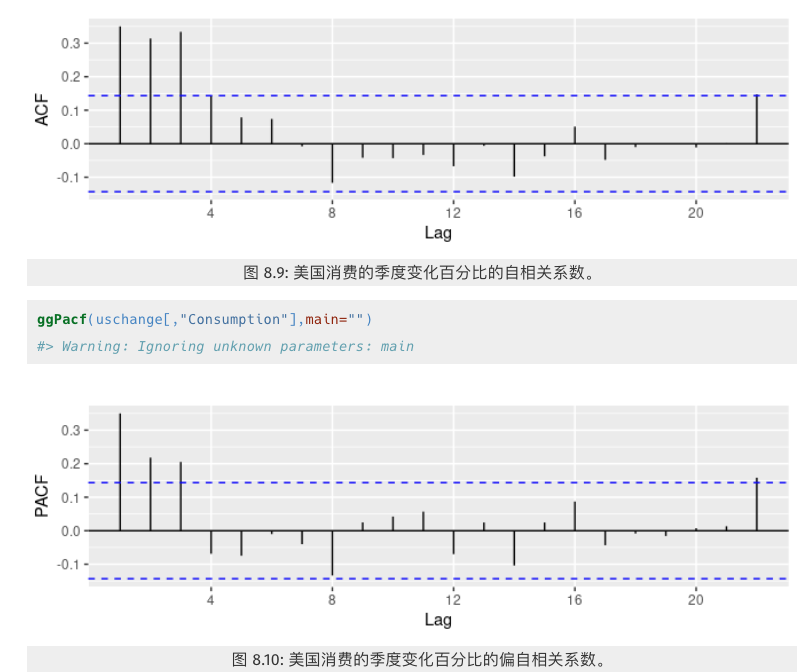
- 如果数据来自于$ARIMA(p,d,0)$或者 $ARIMA(0,d,q)$ 模型,则自相关图和偏自相关图在判定$p$或者$q$的取值时非常有用;
- 如果 $p 和 q$ 都为正,则这些图在寻找最合适的 $p和q$ 值时不再有用;
如果差分数据的自相关图和偏自相关图显示出如下特征,则他们可能来自于$ARIMA(p,d,0)$模型:
- 自相关系数呈现指数下降或者类似正弦型的波动;(拖尾,Tail Off)
- 偏自相关图中的延迟 $p$ 中有明显突起,但延迟更大时不存在类似的突起。(截尾,Cut Off)
如果差分数据的自相关图和偏自相关图数据显示出如下特征,则他们可能来自于$ARIMA(0,d,q)$ 模型:
- 偏自相关系数呈现指数下降或者类似正弦型的波动;(拖尾,Tail Off)
- 在自相关图中的延迟q 中有明显突起,但延迟更大时不存在类似的突起。(截尾,Cut Off)
ACF,PACF 图确定 p, q取值
- 观察哪个图截尾,acf 图或pacf 图。
- 若 PACF 在P阶截尾的,而 ACF 是拖尾的,则建立 $AR(P)$ 模型,即 $ARIMA(P,d,0)$;
- 若 ACF 在Q阶截尾的, PACF 是拖尾的,则建立 $MA(Q)$ 模型,即 $ARIMA(0,d,Q)$;
- 若 ACF 和 PACF 都拖尾,则序列适合ARIMA 模型,即 $ARIMA(P,d,Q)$,其中 P,Q 的值需要进一步确定,如 $(1,d,1), (2,d,1), (2,d,2)$
例1:时序图如下:
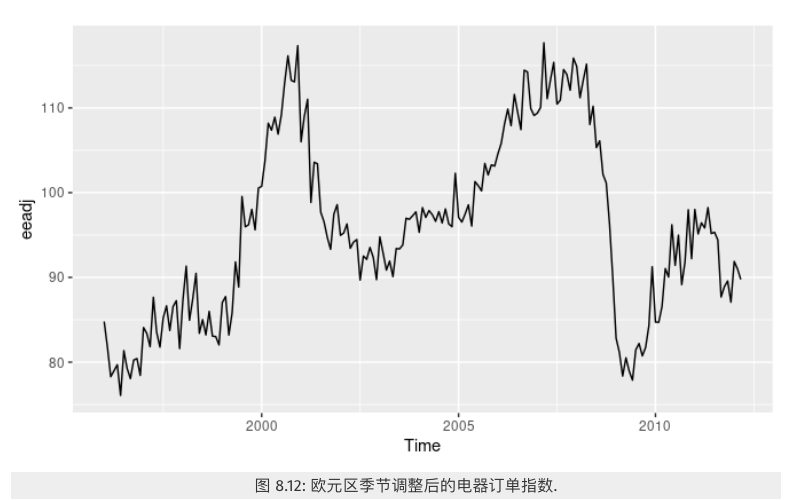
时序图看起来不平稳,做一阶差分后如下图
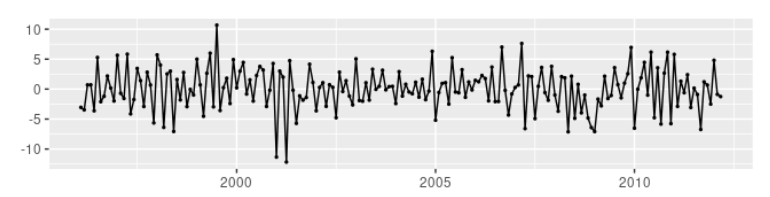
一阶差分后的数据,自相关图以及偏自相关图如下
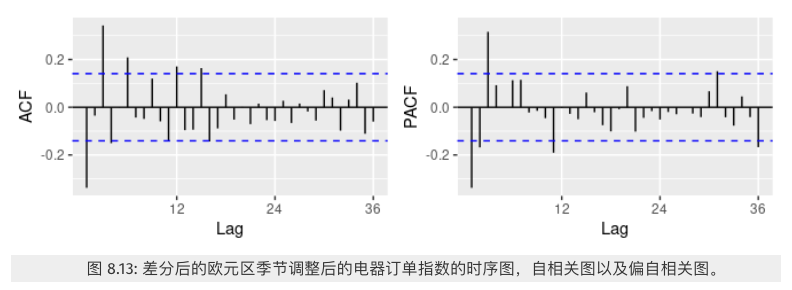
pacf 在3阶截尾,acf拖尾,因此适合AR 模型,即 $ARIMA(3, 1, 0)$。
我们使用 $ARIMA(3,1,0)$以及衍生模型 $ARIMA(4,1,0),ARIMA(2,1,0),ARIMA(3,1,1)$ 等等进行拟合,在这些模型中,$ARIMA(3,1,1)$ 是 $AIC_c$ 值最小的模型。
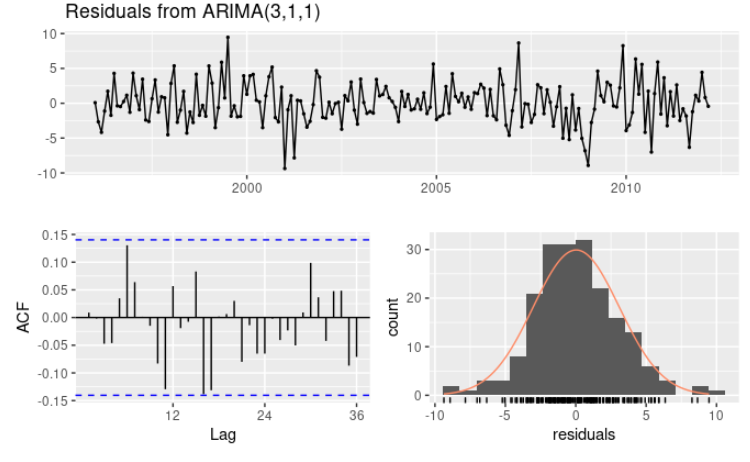
$ARIMA(3,1,1)$ 模型的残差自相关图(如下)显示出所有的自相关系数都在置信域之内,这反映出残差类似于白噪声;
一元混成检验(另外一篇文章简介)得到了一个较大的p值,同样意味着残差类似白噪声。
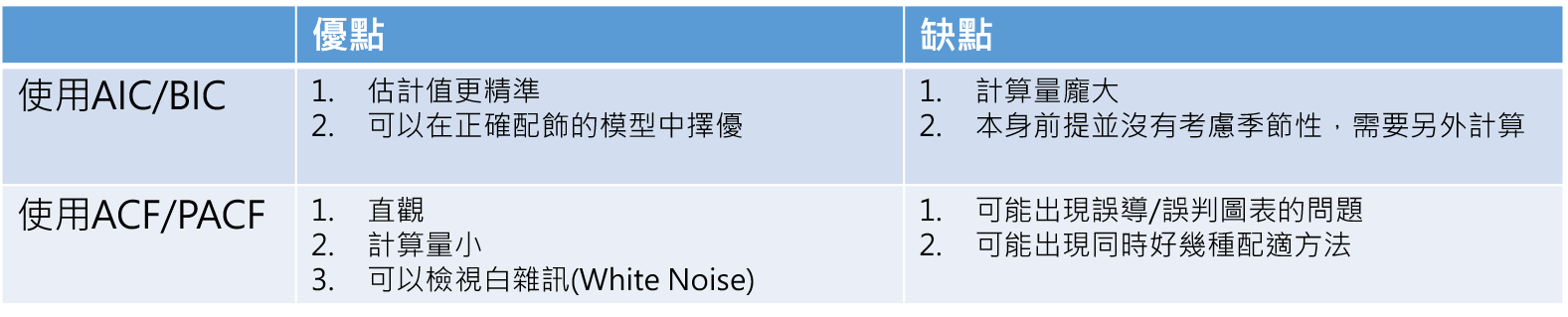
最小化AIC,确定p,q 取值
Hyndman-Khandakar算法流程: