平稳性
如果时间序列的性质不随时间变化而变化(如均值0,方差趋于稳定值),我们称该序列是平稳的。典型的平稳序列是白噪声(white noise series)。
因此具有趋势、周期性、季节性的序列不是平稳序列。
ARIMA模型要求序列是平稳的,或可以通过处理(如差分)平稳化。
判断平稳性
判断平稳性主要有两种,观察法和单位根检验法。
- 观察可视化的数据,从中推断数据是否稳定。如观察时间曲线图或自相关图
- 单位根检验的方法有很多种,如 ADF检验。
观察法
观察曲线图,判断哪些序列平稳
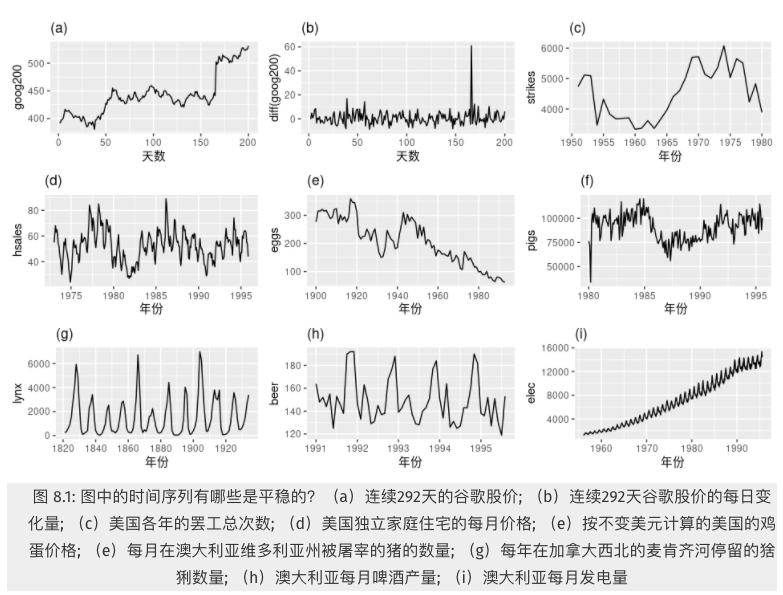
- 存在季节性的序列:d, h, i
- 存在趋势的序列:a, c, e, f, i
- 方差明显变化的序列: i
剩下的 b, g 是平稳序列。
和时间曲线图一样,自相关图(ACF图)也能帮助我们识别非平稳时间序列。 对于一个平稳时间序列,自相关系数(ACF)会快速的下降到接近 0 的水平,然而非平稳时间序列的自相关系数会下降的比较缓慢。
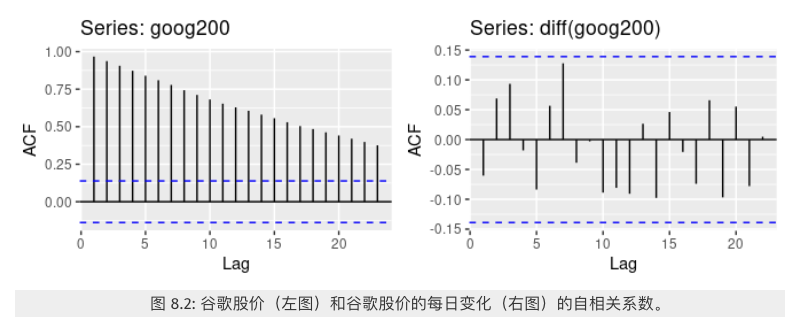
差分后的谷歌股价的自相关图看起来像白噪声序列。所有自回归系数都在 95% 的置信度以内。
- 待更新
平稳化处理方法
平稳性是时间序列分析的前提条件,故我们需要对不平稳的序列进行处理将其转换成平稳的序列。常用的方法有:
- 对数变换
- 平滑法
- 差分
- 分解
差分
差分可以通过去除时间序列中的一些变化特征来平稳化它的均值,并因此消除(或减小)时间序列的趋势和季节性。
差分序列是指原序列的连续观测值之间的变化值组成的时间序列,它可以被表示为:
$$
y_t’ = y_t - y_{t-1}
$$
一阶差分、白噪声、random walk
$$
y_t’ = y_t - y_{t-1}
$$
当差分序列$y’_t$是白噪声时,即可得到“随机游走”模型:
$$
y_t = y_{t-1} + \epsilon_t=y_0 +\sum_{i=1}^{t}\epsilon_i
$$
其中 $\epsilon_t$ 是白噪声。
二阶差分
有时差分后的数据仍然不平稳,所以可能需要再一次对数据进行差分来得到一个平稳的序列:
$$
y_t’’=y_t’ - y_{t-1}’=(y_t - y_{t-1}) - (y_{t-1} - y_{t-2})=y_t-2y_{t-1} + y_{t-2}
$$
季节性差分


