朴素贝叶斯

朴素贝叶斯方法是基于贝叶斯定于和特征条件独立假设的分类方法。

对于给定的训练数据集

1. 首先基于条件独立假设学习输入输出的联合概率分布；
2. 然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出 y。

朴素贝叶斯法优点

• 实现简单
• 学习与预测效率都高

基本方法

朴素贝叶斯法国训练数据学习联合概率分布$P(X = x, Y = y)$。

$$P(X=x, Y=c_k)=P(X=x) * P(Y=c_k|X=x)=P(Y=c_k) * P(=X=x|Y=c_k)$$

具体的计算先验概率分布$P(Y=c_k)$ 和 条件概率分布$P(X=x|Y=c_k)$。

计算条件概率分布 $P(X=x|Y=c_k)$ 是有困难（有指数级数量的参数），如：

• 假设 X 是[m, n]维数据，即训练集有n个特征，每一个是离散型变量，特征$X^{(n)}$ 有$S_n$ 种取值；
• Y是[m, 1]维数据，Y 是离散型变量，取值为c_k，有 K 种取值；
• 那么条件概率分布 $P(X^{(1)}=x^{(1)}, X^{(2)}=x^{(2)},… X^{(n)}=x^{(n)}|Y=c_k)$ 中参数个数为 $K * \prod_{i=0}^n{S_n}$

于是，朴素贝叶斯对条件概率分布做了条件独立性假设，使用离散型独立变量的联合分布计算公式
$$P(A, B)=P(A) * P(B)$$
$$P(A, B|C)=P(A|C) * P(B|C)$$
具体的条件独立性假设如下：

$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)}, X^{(2)}=x^{(2)},… X^{(n)}=x^{(n)}|Y=c_k)=\prod_{j=1}^jP(X^{(j)}=x^{(j)}|Y=c_k)$

特征之间相互独立，意味着每个特征独立的对结果产生影响。条件独立性假设在实际应用中是不现实的，因此得名“朴素“贝叶斯。

对于给定的 x，使用学习到的模型计算后验概率分布 $P(Y=c_k|X=x)$，将后验概率最大的类 C作为x的分类结果输出。后验概率使用贝叶斯公式计算：
$$P(Y=c_k|X=x) = \frac{P(X=x|Y=c_k) * P(Y=c_k)}{P(X=x)}$$

其中，转化一下$P(X=x)$
$$P(X=x) = \sum_{k=1}^{k}P(X=x, Y=c_k)=\sum_{k=1}^{k}P(X=x|Y=c_k) * P(Y=c_k)$$
于是后验概率计算公式变为：
$$P(Y=c_k|X=x) = \frac{P(X=x|Y=c_k) * P(Y=c_k)}{\sum_{k=1}^{k}P(X=x|Y=c_k) * P(Y=c_k)}$$

其中，已计算得先验概率$P(Y=c_k)$、 条件概率分布 $P(X=x|Y=c_k)=\prod_{j=1}^jP(X^{(j)}=x^{(j)}|Y=c_k)$

于是朴素贝叶斯分类器可表示为：
$$y=f(x)=\underset{c_k}{\operatorname{argmax}}\frac{P(Y=c_k) * P(X=x|Y=c_k)}{\sum_{k=1}^{k}P(Y=c_k) * P(X=x|Y=c_k)}$$
$$=\underset{c_k}{\operatorname{argmax}}\frac{P(Y=c_k) * \prod_{j=1}^jP(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_{k=1}^{k}P(Y=c_k) * \prod_{j=1}^jP(X^{(j)}=x^{(j)}|Y=c_k)}$$

因为，对于所有$Y=c_k$分母都是相同的，所以可简写为：

$$y=f(x)=\underset{c_k}{\operatorname{argmax}}P(Y=c_k) * \prod_{j=1}^jP(X^{(j)}=x^{(j)}|Y=c_k)$$

学习与分类算法

输入数据 $T={(x_1, y_1), (x_2, y_2), (x_3, y_3), … (x_N, y_N) }$，其中 $x_i=(x_i^{(1)}, x_i^{(2)}, x_i^{(3)}, … x_i^{(n)})$，$x_i^{(j)}$ 是第i个样本第j个特征，$x_i^{(j)}\in {a_{j1}, a_{j2}, a_{j3}, … a_{jS_j} }$，a_{jl} 是第j个特征可能取的第l个值，$j=1,2,3,…,n$，$l=1,2,3,…,S_j$，$y_i \in {c_1, c_2, c_3, …, c_K}$；实例 $x$

问题：求实例 $x$ 所属分类

答题思路：

1. 计算先验概率和条件概率
   $$P(Y=c_k)= \frac{\sum_{i=1}^{N}I(y_i=c_k)}{N}, k=1,2, …, K$$

$$P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^NI(x_i^{(j)}=a_{jl}, y_i=c_k)}{\sum_{i=1}^{N}I(y_i=c_k)}, \\
j=1, 2, …, n;l=1,2,…,Sj;k=1,2,…, K$$
2. 对于给定的实例 $x_i=(x_i^{(1)}, x_i^{(2)}, x_i^{(3)}, … x_i^{(n)})$，计算朴素贝叶斯分类器：
$$y=f(x)=\underset{c_k}{\operatorname{argmax}}P(Y=c_k) * \prod_{j=1}^JP(X^{(j)}=x^{(j)}|Y=c_k)$$

习题1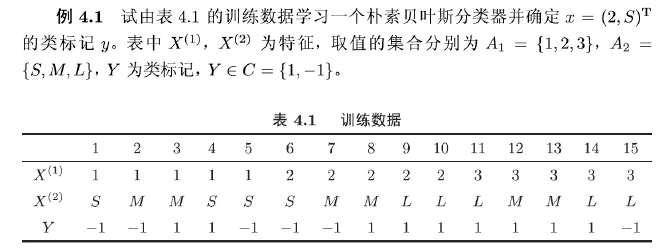

贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0的情况。这会影响后验概率的计算结果，使之产生偏差。解决这一问题的方法是采用贝叶斯估计。

条件概率的贝叶斯估计如下：
$$
P_\lambda(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^NI(x_i^{(j)}=a_{jl}, y_i=c_k)}{\sum_{i=1}^NI(y_i=c_k) + S_j*\lambda}
$$
其中，$\lambda \ge 0$。当$\lambda = 0$时就是极大似然估计。常取$\lambda=1$，这时称为拉普拉斯平滑（Laplacian smoothing）

类似，先验概率的贝叶斯估计如下：
$$
P_\lambda(Y=c_k)=\frac{\sum_{i=1}^NI(y_i=c_k) + \lambda}{N + K\lambda}
$$

总结

朴素贝叶斯法是典型的生成学习方法。

1. 由训练数据学习联合概率分布$P(X, Y)$
   1. 由训练数据学习 $P(X|Y)$ 和 $P(Y)$的估计，从而得到联合概率分布。
      1. 估计$P(X|Y)$时假设条件独立以降低计算困难。因为这个假设，模型需要计算的条件概率的量大大减少，朴素贝叶斯法的学习和训练大为简化。当然同时牺牲了一些分类准确率。
   2. 概率估计可以用极大似然估计或贝叶斯估计。
2. 然后使用贝叶斯公式求得后验概率分布 $P(Y|X)=\frac{P(X, Y)}{P(X)}$。
3. 将输入 x 分到后验概率最大的类 y。后验概率最大相当于 0-1 损失函数时的期望风险最小化。
   $$
   y= \underset{c_k}{\operatorname{argmax}}P(Y=c_k) * \prod_{j=1}^JP(X^{(j)}=a_{jl}|Y=c_k)
   $$

参考文献

• 《统计学习方法》-李航