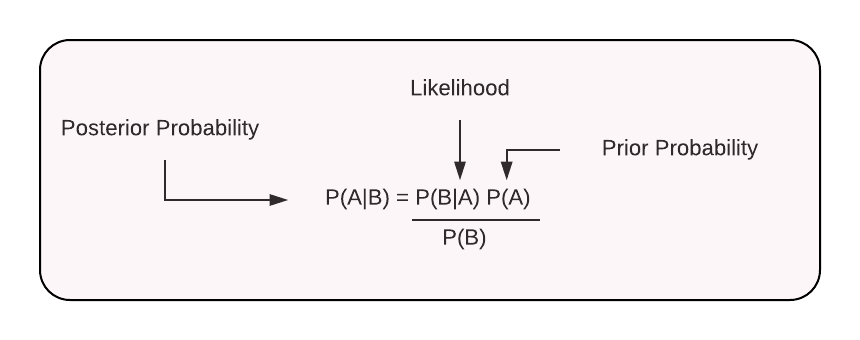
贝叶斯决策论
贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。
极大似然估计
估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布,再基于训练样本对概率分布的参数进行估计。
朴素贝叶斯分类器
不难发现,基于贝叶斯公式来估计后验概率 P(c|x) 的主要困难在于:类条件概率P(x|c) 是所有属性上的联合概率,难以从有限的训练样本直接估计而得。为避开这个问题,朴素贝叶斯分类器(naive Bayes classifier)采用了”属性条件独立性假设“(attribute conditional independence assumption):对已知类别,假设所有属性相互独立。换言之,假设每个属性独立地对分类结果产生影响。
半朴素贝叶斯分类器
为了降低贝叶斯公式中估计后验概率的困难,朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立。于是,人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了一类称为”半朴素贝叶斯分类器“(semi-naive Bayes classifiers) 的学习方法。
贝叶斯网
贝叶斯网(Bayesian Network)也称信念网 (Belief Network),它借助有向无环图(Directed Acyclic Graph, 简称 DAG)来刻画属性之间的依赖关系,并使用条件概率表(Conditional Probability Table,简称 CPT)来描述属性的联合概率分布。
EM算法
现实应用中往往会遇到”不完整“的训练样本。在这种数据不完整情况下,是否仍能对模型参数进行估计呢?
数据缺失的变量称”隐变量“(latent variable)。
EM(Expectation-Maximization)算法是常用的估计参数隐变量的利器。它是一种迭代式方法。
阅读材料
- 《机器学习》-周志华