先验概率和后验概率

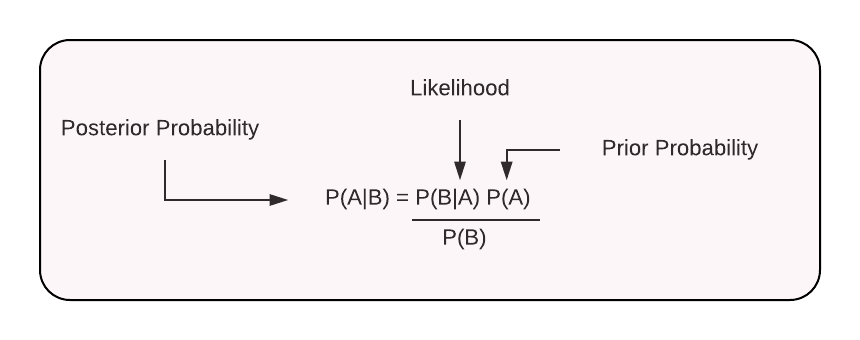
讲解先验概率（Prior probability）和后验概率（Posterior probability）最好的方法是举例子。

例子 1

一般情况下发生了交通事故，更容易堵车。

• 先验概率：今天出门堵车的可能性 $P(堵车)$

• 条件概率：新闻上说发生了交通事故，今天出门堵车的概率 $P(堵车|交通事故)$

• 后验概率：已经堵车了，有发生交通事故的概率 $P(交通事故|堵车)$

例子 2

玩lol占总人口60%，不玩lol的人占40%；

先验概率：$P(X=玩lol)=0.6；P(X=不玩lol)=0.4$

玩 lol 人中80%是男性，20%是女性；不玩 lol 人中20%是男性，80%是女性

条件概率分布：

• $P(Y=男性|X=玩lol)=0.8；P(Y=女性|X=玩lol)=0.2$

• $P(Y=男性|X=不玩lol)=0.2；P(Y=女性|X=不玩lol)=0.8$

那么已知玩家为男性的情况下，他是lol玩家的概率是多少？

依据贝叶斯准则可得：

$P(X=玩lol|Y=男性) = \frac{P(Y=男性|X=玩lol) * P(X=玩lol)}{P(Y=男性|X=玩lol) * P(X=玩lol) + P(Y=男性|X=不玩lol) * P(X=不玩lol)}$

最后算出的 $P(X=玩lol|Y=男性)$ 称之为X的后验概率，即它获得是在观察到事件Y发生后得到的。