随机森林

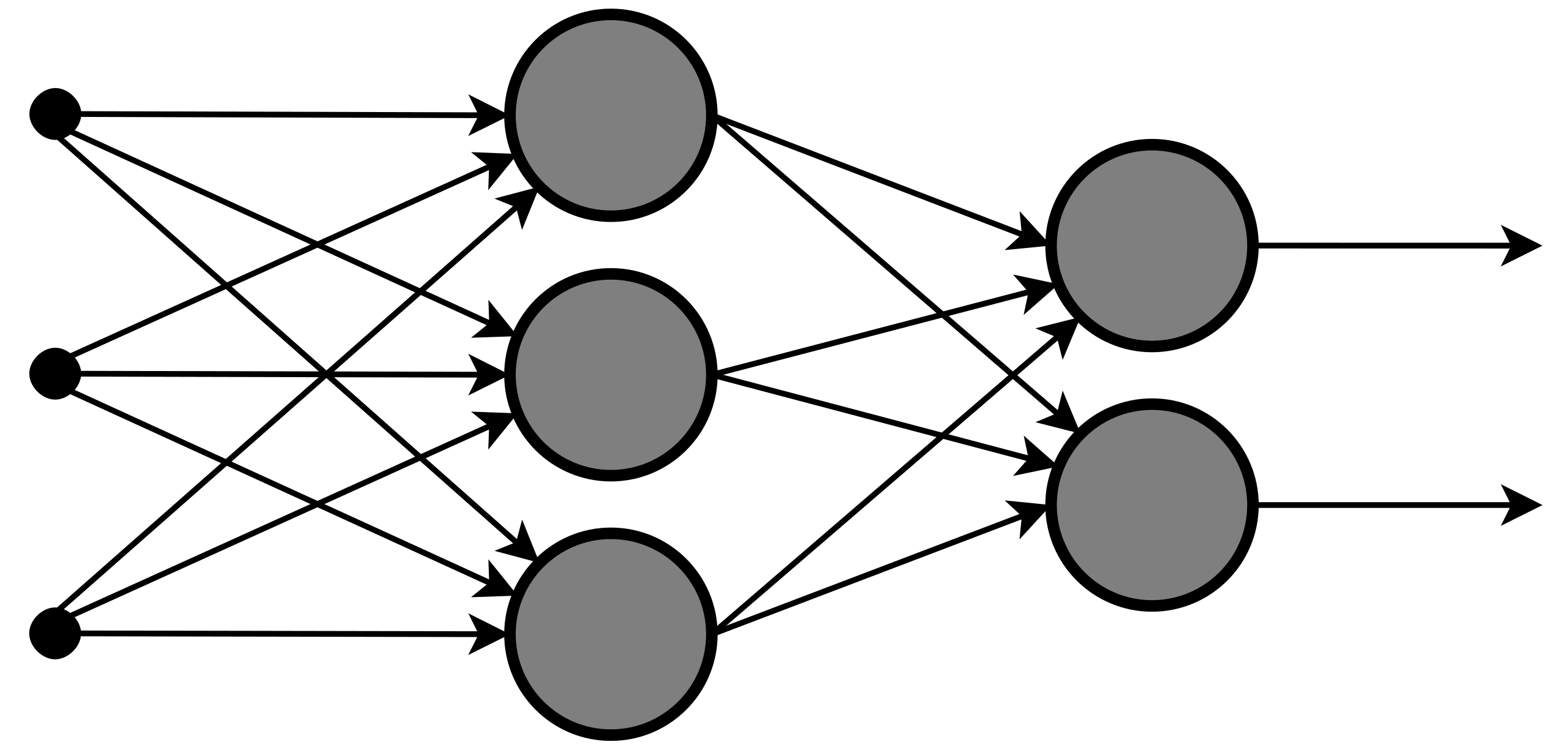
随机森林是一种具有代表性的 Bagging（装袋法）集成算法。

工作原理

把 n 个基评估器的结果，汇总后得到集成算法的结果，以此得到比单个评估器更好的模型表现。

• 其中每个基评估器都是决策树，所以称呼森林；
• 随机挑选特征和数据，生成 n 个决策树，所以称随机。

相关概念

• Bootsrap：随机森林通过有放回的随机抽样技术来形成不同的训练数据，bootsrap等于 TRUE，表示使用这种抽样技术。
  • 含有n个样本的数据集中，进行有放回随机采样n 次，组成大小为n的自助集。
  • 由于有放回随机采样，每个自助集都不同，训练的决策树也不同。
  • 由于有放回采样，有些数据样本会被多个自助集采到、有些数据集始终不会被采到。
• Out of Bag：一般来说，自助集平均包含 63%的原始数据。每个样本被抽到某个自助集中的概率为 1 - (1 - 1/n)^n 。当 n 足够大时，这个概率收敛于 1 - 1/e, 约等于 0.632。因此会有 37% 的训练数据被浪费掉，没有参与建模，这些数据被称为袋外数据(out of bag data, 简写 OOB)。
  • 除了最初划分为测试集的数据之外，这部分OOB数据也可以加入到测试集中。
  • 当然，使用随机森林时，我们可以不划分测试集和训练集，只需要用袋外数据作为测试集即可。（当n 和 n_estimators 都不够大时，很可能就没有oob数据）

相关问题

1. 常用的集成算法有哪些？
   1. Bagging （装袋）法：基评估器互相独立、平行。代表算法是随机森林
   2. Boosting （提升）法：基评估器有顺序，逐渐提升。代表算法有 XGboost
   3. Stacking 法
2. 随机森林用了什么方法，来保证集成的效果一定好于单个分类器?
   1. 例如随机森林中有25棵树，每棵树分类错误的概率是 0.2
   2. 当且仅当13及以上的树都分类错误时随机森林集成结果才分类错误
   3. 13都分类错误的概率：
      
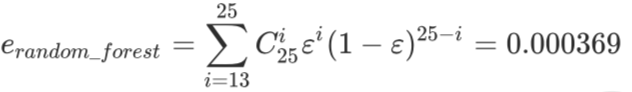
3. 随机森林如何保证，每一个决策树都不一样？（随机性）
   1. 有放回随机抽样训练数据，训练决策树
   2. 随机选择部分特征，构造决策树
4. 使用随机森林有什么特殊要求？
   1. 要求每个基评估器都相互独立；
   2. 基分类器的分类准确率要超过随机分类器（即，随机森林使用的基分类器的准确率至少要超过50%）。当基分类器的误差率小于0.5，即准确率大于0.5 时，集成的效果是比基分类器要好的。相反， 当基分类器的误差率大于0.5，袋装的集成算法就失效了。