- 比较感知机的对偶形式与线性可分支持向量机的对偶形式
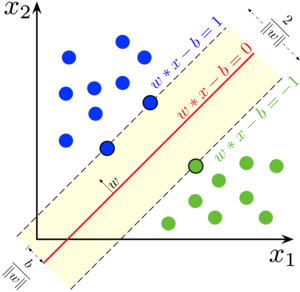
- 已知正例点$x_1=(1,2)^T$,$x_2=(2,3)^T$,$x_3=(3,3)^T$,负例点$x_4=(2,1)^T$,$x_5=(3,2)^T$,试求最大间隔分离超平面和分类决策函数,并在图上画出分离超平面、间隔边界及支持向量
- **线性支持向量机还可以定义为以下形式,试求其对偶形式:
$$\min_{w,b,\xi}{\frac{1}{2}|w|^2}+C\sum^N_{i=1}\xi_i^2\s.t.{\quad}y_i(w{\cdot}x_i+b)\ge1-\xi_i,,i=1,2,\cdots,N\\xi_i\ge0,,i=1,2,\cdots,N$$
- 证明内积的正整数幂函数$K(x,z)=(x{\cdot}z)^p$是正定核函数,这里$p$是正整数,$x,z{\in}R^n$
- 自己编程实现SVM,并在西瓜数据集 3.0αα 测试。
- 试证明样本空间中任意点 $x$ 到超平面 $(w,b)$ 的的距离为式 (6.2)。
- 试使用 LIBSVM,在西瓜数据集 3.0α 上分别用线性核和高斯核训练一个 SVM,并比较其支持向量的差别。
- 选择两个 UCI 数据集,分别用线性核和高斯核训练一个 SVM,并与BP 神经网络和 C4.5 决策树进行实验比较
- 试讨论线性判别分析与线性核支持向量机在何种条件下等价。
- 试述高斯核 SVM 与 RBF 神经网络之间的联系。
- 试析 SVM 对噪声敏感的原因。
- 试给出式 (6.52) 的完整 KKT 条件。
- 以西瓜数据集 3.0α 的”密度”为输入”含糖率”为输出,试使用LIBSVM 训练一个 SVR。
- 试使用核技巧推广对率回归,产生”核对率回归”。
- 试设计一个能显著减少 SVM 中支持向量的数目而不显著降低泛化性能的方法。