- 简述一下K-means算法的原理和工作流程
- 输入k,表示数据聚类到k簇
- 随机选出 k个质心
- 将每个点归到距离最近的质心所属簇
- 求簇中每个点均值,求出该质心新的位置
- 循环3、4
- 当质心不再发生变化停止迭代
- K-means中常用的到中心距离的度量有哪些?
- 欧几里得距离
- 曼哈顿距离
- 余弦相似度
- K-means 中的k值如何选取?
- 随机选取,画出k和轮廓系数(Silhouette Coefficient)的学习曲线,选择最佳k值
- 手肘法:
- K-means 算法中初始点的选择对最终结果有影响吗?
- 不同的初始值结果可能不一样
- 对计算速度有影响。更好的选取初始点,可以加快聚类速度
- K-means 聚类中每个类别中心的初始点如何选择?
- 随机选择初始质心
- 不停更新质心,求出更佳中心
- K-means 中空聚类的处理
- 选择一个距离当前任何质心最远的点。这将消除当前对总平方误差影响最大的点。
- 从具有最大SSE的簇中选择一个替补的质心,这将分裂簇并降低聚类的总SSE。如果有多个空簇,则该过程重复多次。
- 如果噪点或者孤立点过多,考虑更换算法,如密度聚类
- K-means 是否会一直陷入选择质心的循环停不下来?
- 不会,有数学证明Kmeans一定会收敛,大概思路是利用SSE的概念(也就是误差平方和),即每个点到自身所归属质心的距离的平方和,这个平方和是一个凸函数,通过迭代一定可以到达它的局部最优解。(不一定是全局最优解)
- 但同时为了让模型更快,可以设置:
- 迭代次数设置
- 设定收敛判断距离
- 如何快速收敛数据量超大的 K-means?
- 方法1:洗牌后的数据,先选区部分数据,求出质心,确定局部最佳 k 值;使用上述求出的质心,作为初始质心,聚类全量数据
- 方法2:Mini Batch Kmeans使用了一种叫做Mini Batch(分批处理)的方法对数据点之间的距离进行计算。Mini Batch的好处是计算过程中不必使用所有的数据样本,而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本数量少,所以会相应的减少运行时间,但另一方面抽样页必然会带来准确度的下降。
- K-means算法的优点和缺点是什么?
- 缺点:
- 需要人为输入 k值,且很难确定;
- 局部最优;
- 对噪音和异常点敏感;
- 需样本存在均值(限定数据种类);
- 聚类效果依赖于聚类中心的初始化;
- 对于非凸数据集或类别规模差异太大的数据效果不好
- 优点:
- 简单、易于理解、实现容易;
- 可解释性强;
- 基于少量数据也可达到较好效果。
- 缺点:
- 如何对K-means聚类效果进行评估?
- 簇内距离最小化,簇外距离最大化
- 计算每个点轮廓系数;观察每个类中各个点轮廓系数分布
- a是Xi与同簇的其他样本的平均距离,称为凝聚度
- b是Xi与最近簇中所有样本的平均距离,称分离度
- 1 - a/max(a,b)
- 当 a==b,轮廓系数=0,说明这两个簇中数据应该属于同一个簇
- a > b, 轮廓系数负数,说明聚类效果不好
- a < b ,轮廓系数越接近1,说明聚类效果越好
- K-Means与KNN有什么区别
- KNN是分类算法,K-means是聚类算法;
- KNN是监督学习,K-means是非监督学习
- KNN喂给它的数据集是带Label的数据,已经是完全正确的数据,K-means喂给它的数据集是无label的数据,是杂乱无章的,经过聚类后才变得有点顺序,先无序,后有序。
- KNN没有明显的前期训练过程,K-means有明显的前期训练过程
- K的含义KNN来了一个样本x,要给它分类,即求出它的y,就从数据集中,在X附近找距离它最近的K个数据点,这K个数据点,类别C占的个数最多,就把x的label设为c.
- K-means中K是人工固定好的数字,假设数据集合可以分为k个簇,由于是依靠人工定好,需要一些先验知识。
Previous
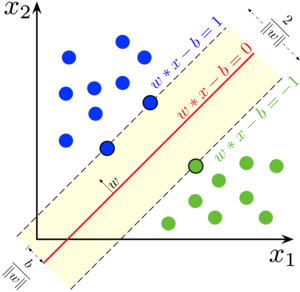 支持向量机内容概要
支持向量机内容概要
2021-01-20
Next
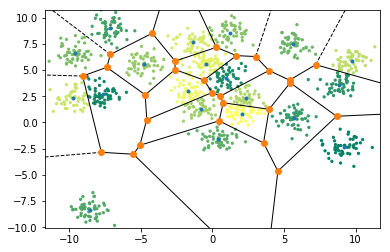 k-means 算法知识点梳理
k-means 算法知识点梳理
2021-01-12