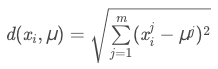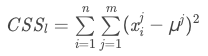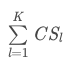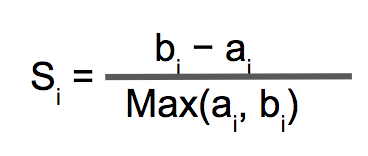k-means 算法知识点梳理

Overview

k-means 算法是最常用的聚类算法，属于无监督学习算法。

工作原理和流程

1. 输入k，表示数据聚类到k簇
2. 随机选出 k个质心（Centroid）
3. 将每个点归到距离最近的质心所属簇
4. 求簇中每个点均值，求出该质心新的位置
5. 循环3、4
6. 当质心不再发生变化停止迭代

特点

1. 最大的特点是简单、好理解
2. 只能应用于连续型的数据，因此对一些数据集需要先处理
3. 要在聚类前需要手工指定要分成几类

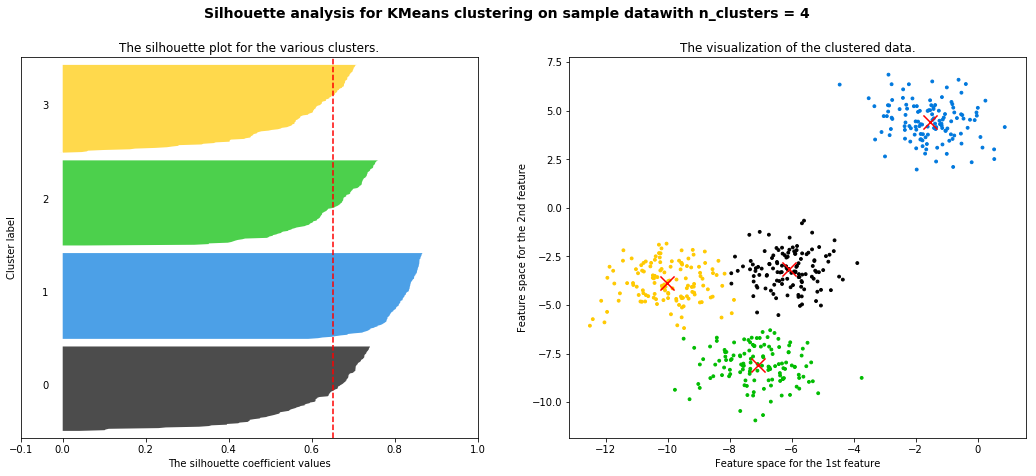
如何评估？

KMeans的目标是确保“簇内差异小，簇外差异大。

使用轮廓系数同时衡量：

1. 样本与其自身所在的簇中的其他样本的相似度 a，等于样本与同一簇中所有其他点之间的平均距离
2. 样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离
   

1. 值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似
2. 当样本点与簇外的样本更相似的时候，轮廓系数就为负。
3. 当轮廓系数为0时，则代表两个簇中的样本相似度一致，两个簇本应该是一个簇。
4. sklearn中，我们使用模块metrics中的类 silhouette_score 来计算轮廓系数，它返回的是一个数据集中，所有样本的轮廓系数的均值。但我们还有同在metrics模块中silhouette_sample，它的参数与轮廓系数一致，但返回的是数据集中每个样本自己的轮廓系数。

相关公式

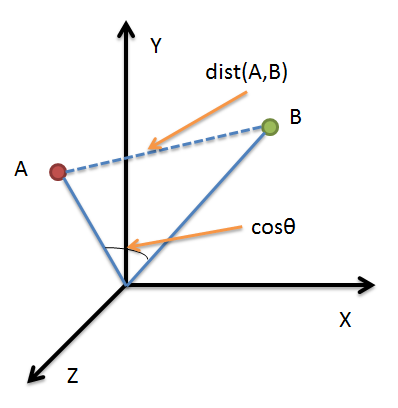
每个点分配到距离最近的质心所属簇。几种距离计算方式：

1. 欧几里得距离
   1. 
   2. 
   3. 
2. 曼哈顿距离
   1. 
3. 余弦相似度：用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小
   1. 

画图分析

1. scatter 聚类图
2. 每个点的轮廓系数柱状图