分类决策树中,我们的目标函数是最大化每次切分数据带来的信息增益:
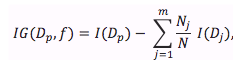
其中 $f$ 是决策问题基于的特征;$D_p$ 和 $D_j$ 分别是父节点数据集和第 $j$ 个子节点数据集; $I$ 不纯度衡量指标; $N$ 是数据集总大小,$N_j$ 是第 $j$ 个子节点上数据集大小。
分类树衡量切分数据集方案好坏的的标尺,最常用的是基尼不纯度(gini impurity)和信息熵(entropy)。另外,有些地方也会用 Classification Error ($I_E$)。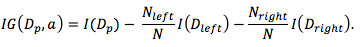
信息熵的定义如下:
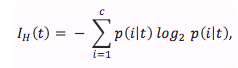
for all “non-empty” classes
共有 C 种分类,且每个类型对于的数据集不全为空的数据集中
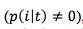
$p(i|t)$ 是 $t$ 节点上属于分类 $i$ 的数据集所占的比例;如果一个节点上所有数据属于单个类型,该节点上数据集的信息熵是 0;如果一个节点上的所有数据均匀分布于不同类型,该节点上数据集的信息熵是最大;
基尼不纯度可被当做衡量最小化数据切分错误的概率的指标。
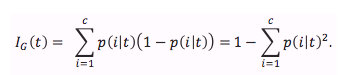
实际应用中,使用基尼系数还是信息熵作为衡量指标,生成的决策树差别不会太大,因此时间应该更多的花在不同剪枝策略的实验上。
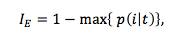
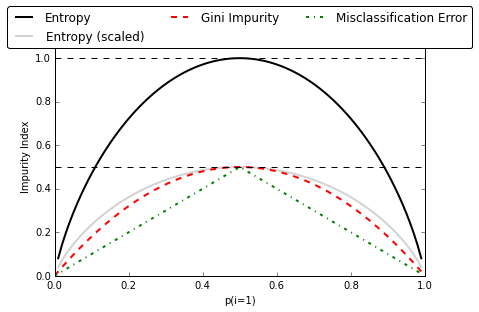
上图可见,Classification Error 对节点上某个类型所占比例的变化不是很敏感,因此不太适合作为目标函数,用来衡量剪枝效果倒是可以。
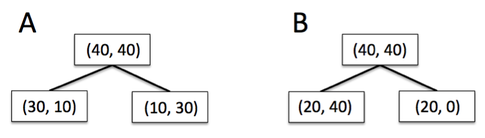
假设数据集 $D_p$ 中 40条数据属于类型1,1条数据属于类型2,对比A、B 两种切分数据集的方案。
可发现,使用 Classification Error 作为目标函数时,A()、B 两种方案的信息增益一样,都是 $IG_E = 0$,无法衡量出哪个方案更好。
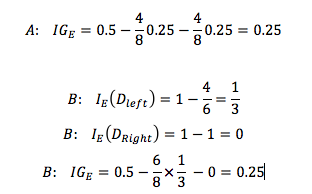
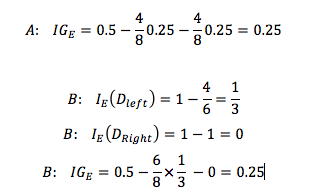
使用 Gini Impurity 作为目标函数时,正确衡量(和不纯度变化一致)出 A(0.125)方案信息增益比B(0.1666)方案小。
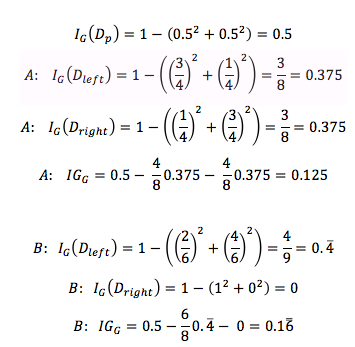
使用 entropy 作为目标函数时,也正确衡量(和不纯度变化一致)出 B(0.31)方案信息增益比 A(0.19)方案大。
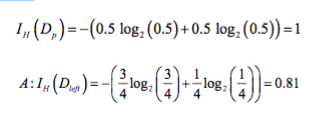
因此,
- 信息熵对数据集的不纯度更加敏感(原因见上图 ),因此决策树的生长会更加“精细”,对于高维数据或者噪音很多的数据,很容易过拟合;
- 信息熵的计算比基尼系数缓慢一些,因为基尼系数的计算不涉及对数。
