决策树介绍

什么是决策树

决策树是一种用树结构进行学习、预测的监督学习方法。英文 Decision Tree。

树结构包含节点和边。节点可分为根节点、内部节点、叶子节点。如下图

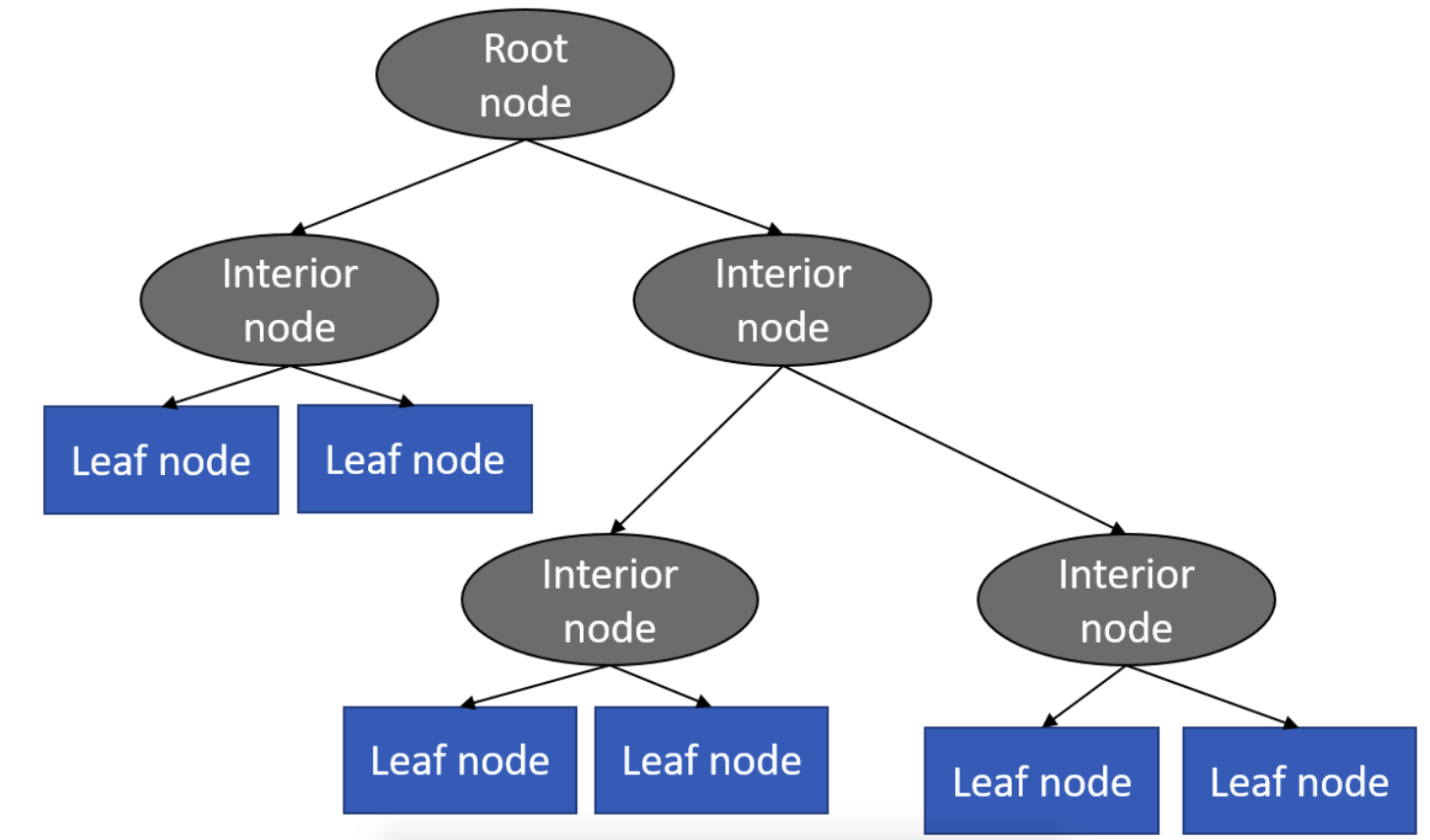
学习（训练）过程：

1. 数据从根节点流入
2. 寻找最佳决策问题，作为切分数据的依据，数据分流入各个边。
3. 如果某一节点上找不到最佳决策问题（或满足停止生长要求），本节点被标为叶子节点并返回。

• 数据不纯度下降最多，作为最佳决策问题的衡量标准。常用基尼系数(gini impurity)和信息熵(entropy)衡量数据不纯度。
• 停止生长要求是为了防止过拟合。

决策树算法遵循“分而治之”的思路。

寻找最佳决策问题序列并生成树的过程就是学习过程。

预测过程：

1. 测试数据流入根节点，依据决策问题分流入边，直至叶子节点。

2. 返回叶子节点的训练数据所属类别作为分类结果。（回归树中，返回叶子节点的训练数据标签均值作为预测结果。

决策树特点

决策数是一种监督学习方法。既可用于分类问题，也可用于回归问题。

决策树的数据（特征和目标数据）可以是离散型，也可以是连续型。

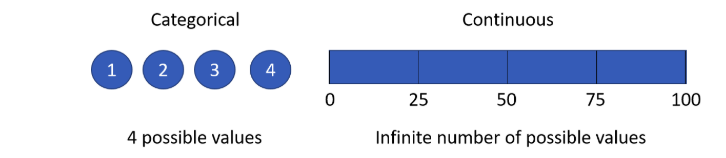
根据目标数据是离散的还是连续，分为分类树和回归树。

决策树属于基于信息的学习算法。

Decision trees are assigned to the information based learning algorithms which use different measures of information gain for learning.

决策树算法

ID3算法原型见于J.R Quinlan的博士论文，是基础理论较为完善，使用较为广泛的决策树模型。
在ID3基础上 J.RQuinlan 进行优化后，陆续推出了C4.5和C5.0决策树算法，后二者现已称为当前最流行的决策树算法。

CART树本质其实和C4.5区别不大，只不过CART树所有的层都是二叉树，
也就是每层只有两个分枝。

决策树算法一般使用递归实现，伪代码如下

参考 决策树工作原理示例

class Node(dta, l_branch=None, r_branch=None):
    self.data = dta
    self.left_branch = l_branch
     self.right_branch = r_branch

bst_tree(data):
    bst_question, left_data, right_data = find_bst_question(data)

    if bst_question 达不到条件:
        return Node(data)

    left_branch = bst_tree(left_data) # <== 递归
    right_branch = bst_tree(right_data) # <== 递归

    tree = Node(data, left_branch, right_branch)
    return tree

基于决策树的集成学习（ensemble learning）方法效果很好，如
装袋法（Bagging）突出代表 Random Forests；提升法（Boosting）突出代表 Adaboost,Gradient Boost,XGBoost。

决策树的优势

1. 白盒，可解释性强

   从根节点到叶子节点的路径就是决策依据

   树形结构容易可视化。

   参考 可视化决策树之Python实现

2. 特征不需要标准化（Normalization）

   特征标准化是为了使不同特征值处于相同的量级范围，不至于出现部分特征主导输出结果的情况。

   简单的决策树来说，计算基尼指数、信息增益等量基于概率值，因此特征值的量级对决策依据没有影响。

3. 既能用于分类问题，也能用于回归问题。

   根据目标数据是离散还是连续的，分为分类树和回归树。

4. 可以建模（捕捉）特征间的非线性(non-linear)关系

   线性(linear)，指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数；如 $k_1X_1+k_2X_2+k_3X_3 + … + k_nX_n=0$，其中$k_n$ 是常数

   非线性(non-linear)则指不按比例、不成直线的关系，一阶导数不为常数。

5. 可以建模（捕捉）不同可解释特征间的相互作用。